待办事项
斜体 的是不会的,加粗的是正在写的,下划线的是暂
- 可重复圆排列(莫比乌斯变换)
- 伯努利数
- 不定方程非负整数解计数
- 容斥原理与第二类 Stirling 数
- 多重组合数 与 多重集的组合数
- 同一列的第二类 Stirling 数计算
- 同一行的第一类 Stirling 数计算
- 同一列的第一类 Stirling 数计算
- Stirling 数通项公式证明
- 恰好 $k$ 部分分拆数与至多 $k$ 部分分拆数
- 分拆数的边界
- 分拆数的五边形数定理
- 群论
- Burnside 引理与 Pólya 定理
排列与组合
加法原理与乘法原理
-
加法原理:多类问题,选择一个。
例如对于一个工程,存在 $n$ 类方法完成,第 $i$ 类方法的方案数为 $a_i$,则总方案数为 $\sum\limits_{i=1}^na_i$。
加法原理的目的就是将原本的 $\sum\limits_{i=1}^na_i$ 种划分为少量易于处理的集合,便于处理。
-
乘法原理:多个步骤,全部完成。
例如转车两次,第一次可选择的车有 $a_1$ 次,第二次有 $a_2$ 次,则最终答案为 $a_1\times a_2$ 次。
常用方法
-
捆绑法:两两相邻时可用,将相邻的部分视为一个整体处理。
例如存在甲乙丙丁四个人排队,要求甲、丁必须站一起,那么可以将甲、丁视作一个人戊,则答案即甲、丁排列的答案乘乙丙戊排列的答案。
-
插空法:要求两两不相邻时可用。
比如有 $A$ 类人 $7$ 人,$B$ 类人 $3$ 人,要求将 $10$ 个人排列,满足 $B$ 类人两两不相邻。
我们可以先排列好 $A$ 类人:
然后我们可以将所有的 $B$ 类人插入 $A$ 类人之间的 $6$ 个空隙中。
总答案即:$7!\times 6\times 5\times 4=604800$ 种方案。
-
隔板法:用于确定不定方程解组个数。
-
对立法:考虑事件对立,用类似于反证法解决。(例子)
排列数与组合数
排列数
从 $n$ 个元素中不重复地选取 $m$ 个不同的元素,按照一定顺序排成一列,称为排列。
排列是有序的。
例如选取 $\lbrace 1,2,3\rbrace $ 和选取 $\lbrace 1,3,2\rbrace $ 就是两个排列。
从 $n$ 个元素中选取 $m$ 个元素的方案数记作 $P_n^m$(读作「$P\ n\ m$」),也可记作 $P(n,m)$ 或 $A_n^m$。
排列的计算公式:
\[P_n^m=n(n-1)(n-2)\cdots(n-m+1)=\frac{n!}{(n-m)!}\]很好理解,选取一个就少一个。
圆排列
若排列成一个圆,则需要注意顺序。
如图:
选取 $\texttt{abcd},\texttt{bcda},\texttt{cdab},\texttt{dabc}$ 形成的圆是一样的。
考虑到这样会有 $m$ 个重复的,因此答案要除以 $m$。
圆排列下,排列的计算公式为:
\[Q_n^m=\frac{n!}{m(n-m)!}\]注:圆排列使用 $Q$。
全排列
在 $n$ 个元素中选取 $n$ 个元素。
答案为:
\[P_n^n=\frac{n!}{0!}=n!\]圆排列时,答案为:
\[P_n^n=\frac{n!}{n}=(n-1)!\]组合数
从 $n$ 个元素中不重复地选取 $m$ 个不同的元素,组成一个集合,称为一种组合。
组合是无序的。
与上文相反,选取 $\lbrace 1,2,3\rbrace $ 和选取 $\lbrace 1,3,2\rbrace $ 就是同一种组合。
从 $n$ 个元素中选取 $m$ 个元素的方案数记作 $\dbinom{n}{m}$,读作「$n$ 选 $m$」,也可记作 $C(n,m)$ 或 $C_n^m$,读作「$C\ n\ m$」。
组合的计算公式为:
\[\binom{n}{m}=\frac{P_n^m}{m!}=\frac{n!}{m!(n-m)!}\]组合数的 $\KaTeX$ 输入
使用 \binom{n}{m} 或 {n\choose m} 来输入 $\binom{n}{m}$。
后一种一定需要加 {} 来保证不会出现错误。
对于 \binom,可以像 \dfrac 一样使用 \dbinom。
理解起来也不难,相同的 $m$ 个元素总共有 $m!$ 种排列,属于一种组合。
允许重复的组合
从一个大小为 $n$ 的集合中取 $m$ 个元素,可以重复取,求有多少种方案。
方案数为:
\[\binom{n+m-1}{m}\]证明:
不妨令集合有序,元素为 $s_1,s_2,s_3,\cdots,s_n$。
令取走的 $m$ 个元素为 $\large s_{a_1},s_{a_2},s_{a_3},\cdots,s_{a_m}$,则有:
\[a_1\leq a_2\leq a_3\leq \cdots\leq a_m\]则:
\[a_1<a_2+1<a_3+2<\cdots<a_m+(m-1)\]因此我们可以在原集合上构造一个新的集合,使得元素一一对应。
最终集合内总元素个数即 $n+(m-1)=n+m-1$。
则原问题等价于从 $n+m-1$ 个元素中不重复地取 $m$ 个元素。
不相邻组合
从一个大小为 $n$ 的集合中不重复地取 $m$ 个不同元素,要求选取的元素互不相邻,求有多少种方案。
方案数为:
\[\binom{n-m+1}{m}\]证明:
不妨令集合有序,元素为 $s_1,s_2,s_3,\cdots,s_n$。
令取走的 $m$ 个元素为 $\large s_{a_1},s_{a_2},s_{a_3},\cdots,s_{a_m}$,则有:
\[a_1<a_2-1<a_3-2<\cdots<a_m-(m-1)\]与上文同理,可以构造一个新集合与原集合内元素一一对应。
最终集合内总元素个数即 $n-(m-1)=n-m+1$。
则原问题等价于从 $n-m+1$ 个元素中不重复地取 $m$ 个元素。
球盒问题
一类经典问题。
将 $n$ 个球放入 $m$ 个盒子,求方案数。
八种经典组合:
- 球:是否有区别
- 盒:是否有区别
- 盒:是否能为空
| 球有无区别 | 盒有无区别 | 盒能否为空 | 方案数 | 注释 |
|---|---|---|---|---|
| 有 | 有 | 能 | $m^n$ | 每个球都有 $m$ 种选择。 |
| 有 | 有 | 否 | \(m!\begin{Bmatrix}n\\m\end{Bmatrix}\) | 第二类 Stirling 数:划分之后进行全排列。 |
| 有 | 无 | 能 | \(\sum\limits_{i=1}^{\min(n,m)}\begin{Bmatrix}n\\i\end{Bmatrix}\) | 第二类 Stirling 数:划分为至多 $\min(n,m)$ 个非空子集的方案数总和。 |
| 有 | 无 | 否 | \(\begin{Bmatrix}n\\m\end{Bmatrix}\) | 第二类 Stirling 数。 |
| 无 | 有 | 能 | $\dbinom{n+m-1}{n}$ | 从 $m$ 个盒中选择 $n$ 个来放入球,可重复,即允许重复的组合。 |
| 无 | 有 | 否 | $\dbinom{n-1}{m-1}$ | 插空法:$n$ 个球摆好,将 $m-1$ 个挡板插入 $n-1$ 个空即可。 |
| 无 | 无 | 能 | $\left[x^n\right]G(x)=\frac{1}{(1-x)(1-x^2)\cdots(1-x^m)}$ | 将 $n$ 个球划分为至多 $m$ 个部分的方案数之和,即分拆数。 |
| 无 | 无 | 否 | $\left[x^n\right]G(x)=\frac{x^m}{(1-x)(1-x^2)\cdots(1-x^m)}$ | 将 $n$ 个球分为恰好 $m$ 个部分,即分拆数。 |
组合数的性质与求解
-
\[\binom{n}{m}=\binom{n}{n-m}\]
证明
从 $n$ 个元素中取 $m$ 个元素,选择的方案数与没被选择的方案数相同。
换而言之,选择 $m$ 个元素的方案数等于选择剩下没被选择的 $n-m$ 个元素的方案数。
-
\[\binom{n}{m}=\frac{n}{m}\binom{n-1}{m-1}\]
证明
代入公式即可。
$$ \binom{n}{m}=\frac{n!}{m!(n-m)!}=\frac{n}{m}\times\frac{(n-1)!}{(m-1)!(n-m)!}=\frac{n}{m}\binom{n-1}{m-1} $$
-
\[\binom{n}{m}=\binom{n-1}{m}+\binom{n-1}{m-1}\]
证明
代数证法:代入公式即可。
组合数证法:
从 $n$ 个元素中取 $m$ 个元素,考虑元素 $a$ 选与不选时的方案。
当元素 $a$ 不选时,方案数即从剩下 $n-1$ 个元素中选 $m$ 个元素的方案数。
当元素 $a$ 选时,方案数即从剩下 $n-1$ 个元素中选 $m-1$ 个元素的方案数。
总方案数即两者相加。
这也说明了一件事:可以通过杨辉三角求解组合数。
事实上,杨辉三角的第 $i$ 行第 $j$ 列就是 $\dbinom{i-1}{j-1}$。
如图:
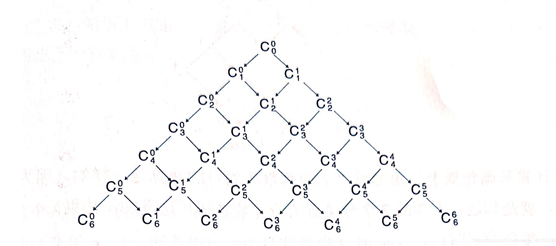
-
\[\binom{n}{m+1}=\frac{n-m}{m+1}\binom{n}{m}\]
展开公式可证。
用于 $\mathcal O(n)$ 递推 $\dbinom{n}{i}$。
重数优化
注:这是在进行高精度操作时的优化,因为高精除麻烦。
重数的定义
对于一个数 $n$,其关于 $p$ 的重数表示其因数中 $p$ 的个数。
对于质数 $p$,即质因子中 $p$ 的个数。
在进行组合数运算时,常常会遇到除法。
而除法效率低下,因此想办法避免。
定义数组 $c$,$c_i$ 表示 $i$ 关于 $n!$ 的重数。
那么就有:
\[\large c_i=\left\lfloor\frac np\right\rfloor +\left\lfloor\frac n{p^2}\right\rfloor +\left\lfloor\frac n{p^3}\right\rfloor +\cdots +\left\lfloor\frac n{p^{\lfloor\log_p n\rfloor}}\right\rfloor\]处理时,操作 $c_i$ 即可。
最终答案即 $\sum\limits_{i=1}^kc_i\times i$。
组合数取模
当模数为质数的时候计算逆元将除法改乘法后求解即可。
其他方法见下文 卢卡斯定理 Lucas 定理 和 扩展卢卡斯定理 exLucas 定理。
排列或组合不存在
从 $n$ 个元素中选择 $m$ 个元素,若 $m>n$ 则不存在方案。
即:当 $m>n$ 时,满足 $\dbinom{n}{m}=P_m^n=0$。
二项式定理
二项式定理描述的是一个展开式:
\[\large (a+b)^n=\sum_{i=0}^n\binom{n}{i}a^{n-i}b^i\]$a,b$ 的项数顺序不影响答案
因为 $\dbinom{n}{i}=\dbinom{n}{n-i}$。因此对于每一个 $i$,都存在一个 $i'=n-i$ 满足 $a^{i}b^{i'},a^{i'}b^i$ 存在,交换顺序不影响答案。
唯一的例外是当 $n$ 为奇数时,会存在一个元素没有“配对”元素,但这也不影响,因为那必定是 $\frac12(n+1)$,$a,b$ 的项数相同。
证明
引理:$(a+b)^n$ 的每一项的次数和均为 $n$
考虑数学归纳法。
$n=0$ 时有 $(a+b)^0=1$,满足次数和为 $1$。
假设 $n=k$ 时,引理成立。
则 $(a+b)^{k+1}=(a+b)(a+b)^k=a(a+b)^k+b(a+b)^k$,显然 $a(a+b)^k$ 展开后每一项的次数和均为 $k+1$,$b(a+b)^k$ 同理。
故,引理成立。
设 $(a+b)^n=\sum\limits_{i=0}^np_ia^ib^{n-i}$。
想要得到 $a^ib^{n-i}$,即从 $n$ 个 $a+b$ 中选出 $i$ 个 $a$,确定 $n-i$ 个 $b$(每一个 $(a+b)$ 会贡献一个 $a$ 或一个 $b$),即 $p_i=\dbinom{n}{i}$。
故:
$$ (a+b)^n=\sum_{i=0}^n\binom{n}{i}a^ib^{n-i} $$
二项式推论
-
\[\binom{n}{0}+\binom{n}{1}+\binom{n}{2}+\cdots+\binom{n}{n}=\sum_{i=0}^n\binom{n}{i}=2^n\]
取 $a=b=1$ 代入即可。
-
\[\sum_{i=0}^n(-1)^i\binom{n}{i}=[n=0]\]
其中 $[n=0]$ 为艾弗森括号,表示条件是否成立,$n=0$ 成立时为 $1$,否则为 $0$。
令 $a=1,b=-1$ 即可。
-
\[\sum_{i=0}^ni\binom{n}{i}=n\times 2^{n-1}\]
令 $a=x,b=1$,代入二项式定理两边求导后可证 $x=1$。
-
\[\sum_{i=0}^ni^2\binom{n}{i}=n(n+1)2^{n-2}\]
同上。
显然我还是不会证明。 -
\[\sum_{i=0}^m\binom{n}{i}\binom{m}{k-i}=\binom{m+n}{k}\]
范德蒙德恒等式。
代入组合数计算公式展开可证。
其推论:
\[\sum_{i=0}^n\binom{n}{i}^2=\binom{2n}{n}\]令 $n=k=m$ 即可。
-
\[\sum_{i=0}^n\binom{i}{k}=\binom{n+1}{k+1}\]
朱世杰恒等式。
考虑集合 $S=\lbrace a_1,a_2,a_3,\cdots,a_{n+1}\rbrace $ 的 $k+1$ 子集数可证。
我还是不会。 -
\[\binom{n}{r}\binom{r}{k}=\binom{r}{k}\binom{n}{r}=\binom{n}{k}\binom{n-k}{r-k}\]
代入公式展开可证。
-
\[\sum_{i=0}^n\binom{n-i}{i}=F_{n+1}\]
$F$ 为斐波那契数列,第一项为 $F_0=0$。
不会证。 -
\[\binom{n+k}{k}^2=\sum_{j=0}^k\binom{k}{j}^2\binom{n+2k-j}{2k}\]
通过范德蒙恒等式可证,被称为李善兰恒等式。
还是不会证。 -
\[\sum_{n=0}^\infty\binom{m}{n}x^n=(1+x)^m\]
多用于求解生成函数的封闭形式。通过二项式定理带入 $a=x,b=1$ 即可得证。
广义牛顿二项式定理
设 $\alpha$ 为一个数,则:
\[(a+b)^\alpha=\sum_{i=0}^{\infty}\dbinom{\alpha}{i}a^ib^{\alpha-i}\]且需要重新定义组合数运算为:
\[\dbinom{\alpha}{i}=\dfrac{\alpha^{\underline{i}}}{i!}\]二项式反演
若 $g_n=\sum\limits_{i=0}^n\dbinom nif_i$,则有:
\[f_n=\sum_{i=0}^n(-1)^{n-i}\dbinom nig_i\]若 $g_n=\sum\limits_{i=n}^\infty\dbinom inf_i$,则有:
\[f_n=\sum_{i=n}^\infty(-1)^{i-n}\dbinom nig_i\]事实上,二项式反演就是容斥原理的特殊形式。
格路问题 路径计数问题
这一部分其实同时包括了“排列与组合”、“生成函数与递推关系”和“容斥原理与鸽巢原理”。但因为后两者涉及较浅,放在“排列与组合”部分。
给定一张网格图,你可以向上走或向右走,每次走一个单位长度,起点为点 $(0,0)$,终点为点 $(m,n)$。
非降路径指代在网格图中只能向上或向右的路径。
如果说,向右的路径称之为“$\texttt x$ 型路径”,向上的路径称之为“$\texttt y$ 型路径”,则如图:
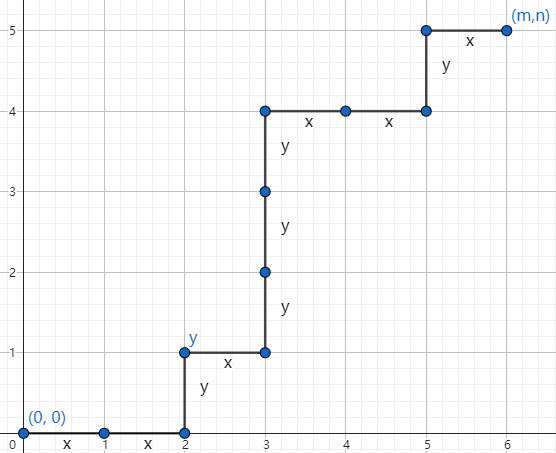
不难发现,在从点 $(0,0)$ 至点 $(m,n)$ 的路径上,无论如何都会有 $m$ 个 $\texttt x$,$n$ 个 $\texttt y$。
因此一条路径就可以表示为 $m$ 个 $\texttt x$ 与 $n$ 个 $\texttt y$ 的排列。图中为 $\texttt{xxyxyyyxxyx}$。
无限制
考虑到 $\texttt x$ 无区别,$\texttt y$ 无区别,且确定其中一个就能确定剩下的,这个排列的数目为 $\dbinom{n+m}{n}=\dbinom{n+m}{m}$,即方案数。
不能触碰直线 $y=x$ 路径端点除外
此部分终点为 $(n,n)$。
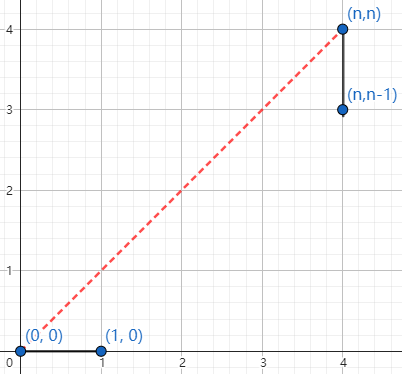
那么就会存在如图中的一条确定的路径。
则问题转化为了:求从点 $(1,0)$ 至点 $(n,n-1)$ 的方案数。
考虑到其等价于从点 $(0,0)$ 至点 $(n-1,n-1)$ 的方案数,则这条路径的总方案数为 $\dbinom{2n-2}{n-1}$。
当这条路径经过了直线 $y=x$ 时,令交点为点 $P$,则可以将从点 $(0,0)$ 至点 $P$ 的部分关于直线 $y=x$ 作对称变换,得到一条等效的新路径。如图:
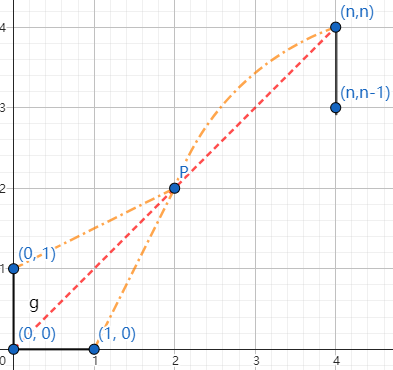
新路径的方案数等价于从点 $(0,0)$ 至点 $(n,n-2)$ 的方案数,为 $\dbinom{2n-2}{n}$。
由容斥原理,总方案数为:
\[\begin{aligned} \binom{2n-2}{n-1}-\binom{2n-2}{n}&=\frac{(2n-2)!}{(n-1)!(n-1)!}-\frac{(2n-2)!}{n!(n-2)!}\\ &=\frac{1}{n-1}\binom{2n-2}{n}\\ &=\frac1n\binom{2n-2}{n-1} \end{aligned}\]这是在直线 $y=x$ 下方时的方案数,若能够在上方,则答案需要乘 $2$,即:
\[\frac2n\binom{2n-2}{n-1}\]不能触碰直线 $y=x+1$
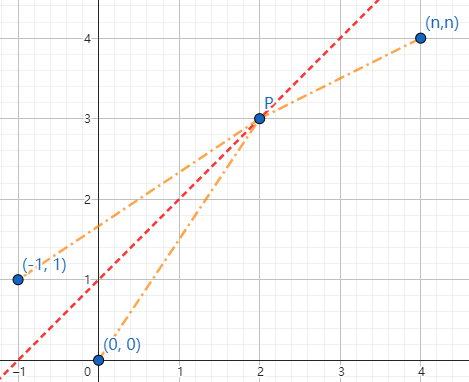
同上文,构造对称。
从点 $(0,0)$ 至点 $(n,n)$ 的路径总数为 $\dbinom{2n}{n}$,从点 $(-1,1)$ 至点 $(n,n)$ 的方案数为 $\dbinom{2n}{n-1}$。
由容斥原理,符合条件的方案数为:
\[\begin{aligned} \binom{2n}{n}-\binom{2n}{n-1}&=\frac{(2n)!}{n!n!}-\frac{(2n)!}{(n-1)!(n+1)!}\\ &=\frac{(2n)!}{n!(n+1)!}\\ &=\frac{1}{n+1}\cdot\frac{(2n)!}{n!n!}\\ &=\frac{1}{n+1}\binom{2n}{n} \end{aligned}\]可以发现,这就是 Catalan 数。
提供一种自己想的还被卡半小时的错误做法。
如图,同上文,存在两条确定路径,且从点 $(1,0)$ 至点 $(n,n-1)$ 的的总方案数为 $\dbinom{2n-2}{n-1}$。
作点 $(1,0)$ 关于直线 $y=x+1$ 的对称点 $(-1,2)$,连接点 $(-1,2)$ 和点 $P$。
从点 $(-1,2)$ 至点 $(n,n-1)$ 的方案数为 $\dbinom{2n-2}{n+1}$。
由容斥原理,符合条件的方案数为: \(\begin{aligned} \binom{2n-2}{n-1}-\binom{2n-2}{n+1} \end{aligned}\)
貌似正确,实则不然——随便代入几组样例即可发现。
主要原因:应当直接对称,强行确定路径导致计数错误。
不能越过直线 $y=x$
即:不能触碰直线 $y=x+1$ 或不能触碰直线 $y=x-1$。
由对称性,两种情况等效。
因此,总方案数为:
\[\frac2{n+1}\binom{2n}{n}\]生成函数与递推关系
母函数 生成函数
生成函数即母函数。
其主要思想是将一个序列 $a_1,a_2,a_3,\cdots,a_n,\cdots$ 与一个函数项级数 $G(x)=\sum\limits_{n=0}^\infty a_nu_n(x)$ 联系起来,从而通过研究 $G(x)$ 得到原序列的性质。
但是,为了便于研究生成函数,且生成函数中的 $x$ 没有意义,因此一般都有 $0<x<1$ 来使得 $x^\infty$ 收敛为 $0$,从而存在封闭形式。
生成函数分为普通生成函数(对应处理组合问题)和指数生成函数(对应处理排列问题)。
几种常见的生成函数:
-
普通生成函数:
\[G(x)=\sum_{n=0}^\infty a_nx^n\] -
指数生成函数:
\[G(x)=\sum_{n=0}^\infty a_n\frac{x^n}{n!}\]
一般来讲,在未特殊声明的前提下,“生成函数”指代的均为普通生成函数。
生成函数 $G(x)$ 中 $x$ 的作用
生成函数中的 $x$ 没有任何作用,就是个占位符。
事实上,我们求解出生成函数最后求解答案时,使用的多为系数。因此 $x$ 可以不管。
当序列 $a$ 有限时,级数求和不应当取 $\infty$ 项,而应当取长度项减一(从 $0$ 开始)。
一道例题
有红球两个,蓝球一个、绿球一个,试求有多少种不同的组合方案?
组合数解法
对于红球,三种选择;对于蓝球,两种选择;对于绿球,两种选择。
则最终组合方案数为 $3\times 2\times 2=12$。
生成函数解法
考虑使用 $x$ 的指数表示球的总数,项的系数对应选择的方案数目。
考虑构造数列 $a_{1,0},a_{1,1},a_{1,2},\cdots,a_{2,0},a_{2,1},a_{2,2},\cdots,a_{3,0},a_{3,1},a_{3,2},\cdots$,每一项都为 $1$。
取红球的生成函数为:
\[\begin{aligned} G_1(x)&=\sum_{n=0}^2 a_{1,n}x^n\\ &=a_{1,0}+a_{1,1}x+a_{1,2}x^2\\ &=1+x+x^2 \end{aligned}\]取蓝球的生成函数为:
\[\begin{aligned} G_2(x)&=\sum_{n=0}^1 a_{2,n}x^n\\ &=a_{2,0}+a_{2,1}x\\ &=1+x \end{aligned}\]取绿球的生成函数为:
\[\begin{aligned} G_3(x)&=\sum_{n=0}^1 a_{3,n}x^n\\ &=a_{3,0}+a_{3,1}x\\ &=1+x \end{aligned}\]则总方案数目的生成函数为:
\[\begin{aligned} G(x)&=G_1(x)\cdot G_2(x)\cdot G_3(x)\\ &=(1+x+x^2)(1+x)(1+x)\\ &=x^4+3x^3+4x^2+3x+1\\ \end{aligned}\]则总方案数目为 $1+3+4+3+1=12$。
基本运算
加减法
考虑序列 $a,b$ 的普通生成函数 $A(x),B(x)$,那么:
\[A(x)\pm B(x)=\sum_{n=0}^\infty(a_n\pm b_n)x^n\]$A(x)\pm B(x)$ 是序列 $\left\langle a_b\pm b_n \right\rangle$ 的生成函数。
乘法 多项式卷积
考虑序列 $a,b$ 的普通生成函数 $A(x),B(x)$,那么:
\[A(x)\cdot B(x)=\sum_{n=0}^\infty\left(\sum_{i=0}^n a_ib_{n-i}\right)x^n\]$A(x)\cdot B(x)$ 即序列 $\left\langle\sum\limits_{i=0}^na_ib_{n-i}\right\rangle$ 的生成函数。
但是这似乎存在问题。
如果使用乘法法则进行运算,则 $A(x)\cdot B(x)$ 应当为:
\[A(x)\cdot B(x)=\sum_{i=0}^\infty\sum_{j=0}^\infty a_ib_j\cdot x^{i+j}\]显然,这个东西算不了。
所以令 $i+j=n$,就可以变换为上面的第一个式子,便于计算。
普通生成函数
普通生成函数用于求解组合问题。
定义序列 $a_1,a_2,a_3,\cdots,a_n,\cdots$ 的普通生成函数为形式幂级数:
\[G(x)=\sum_{n=0}^\infty a_nx^n\]特别地,若序列 $a$ 存在通项公式,那么通项公式即系数 $a_n$。
当然,有些序列不存在形式幂级数形式的生成函数,仅仅存在封闭形式的,因此也不存在通项公式。
生成函数定理
这东西在面试和笔试中比较有用,对 OI 影响似乎不大。
对于 $n$ 元集合 $S=\lbrace a_1,a_2,a_3,\cdots,a_n\rbrace $,若限定元素 $a_i$ 出现次数的集合为 $M_i$,则该组合数序列的生成函数为:
\[\large G(x)=\prod_{i=1}^n\left(\sum_{m\in M_i}p_{i,m}\cdot x^m\right)\]其中,$p_{i,m}$ 为系数,需要依据题目而求。原 PPT 中省略了系数,讲课时也省略了,害我思考好久。。。
下面通过一道例题来辅助理解。
一道例题
某单位有 $8$ 位男同志,$5$ 位女同志。现要组织一个由偶数个男同志和数目不少于两个的女同志组成的小组,试求有多少种组成方式?
此处显然不能像上文那样轻而易举地通过组合数得出答案,但是我们可以通过生成函数来解决。
设男同志组合数序列的生成函数为 $G_1(x)$,女同志为 $G_2(x)$,生成函数中每一项的次数表示选择的人数。
男同志只能选择偶数个,则能够选择的数目的集合为 $M_1=\lbrace 0,2,4,6,8\rbrace $:
\[\large G_1(x)=\binom80x^0+\binom82x^2+\binom84x^4+\binom86x^6+\binom88x^8\]女同志至少选择 $2$ 个,则能够选择的数目的集合为 $M_2=\lbrace 2,3,4,5\rbrace $:
\[\large G_2(x)=\binom52x^2+\binom53x^3+\binom54x^4+\binom55x^5\]则总组合数目的生成函数为:
\[\large \begin{aligned} G(x)&=G_1(x)\cdot G_2(x)\\ &=\left(\binom80x^0+\binom82x^2+\binom84x^4+\binom86x^6+\binom88x^8\right)\left(\binom52x^2+\binom53x^3+\binom54x^4+\binom55x^5\right)\\ &=10x^2+10x^3+285x^4+281x^5+840x^6+728x^7+630x^8+350x^9+150x^{10}+38x^{11}+5x^{12}+x^{13} \end{aligned}\]则最终答案为:
\[\large \begin{aligned} \sum_{n=0}^\infty [x^n]G(x)&=10+10+285+281+840+728+630+350+150+38+5+1\\ &=3328\\ \end{aligned}\]其中 $[x^n]G(x)$ 表示 $G(x)$ 中 $x^n$ 项的系数。
在这个例子中,就是一个二元集合 $S=\lbrace \text{男同志},\text{女同志}\rbrace $。
男同志能够出现的次数的集合 $M_1=\lbrace 0,2,4,6,8\rbrace $,女同志能够出现的次数的集合 $M_2=\lbrace 2,3,4,5\rbrace $。
系数即从男(女)同志中选择出指定人数的方案数,组合数计算即可。
封闭形式
通常情况下,我们会将形式幂级数转换为封闭形式以便于分析。
例如,求解序列 $\dbinom n0,\dbinom n1,\dbinom n2,\cdots,\dbinom nn$ 的封闭形式的母函数。
其母函数显然为:
\[\begin{aligned} G(x)&=\sum_{i=0}^n\dbinom nix^i\\ &=\sum_{i=0}^n\dbinom nix^i1^{n-i}\\ &=(1+x)^n \end{aligned}\]则 $\large (1+x)^n$ 就被称为形式幂级数的封闭形式。
常见生成函数的封闭形式
- $\large \sum\limits_{i=0}^\infty x^i=\dfrac{1}{1-x}$
- $\large \sum\limits_{i=0}^\infty(i+1)x^i=\dfrac{1}{(1-x)^2}$
- $\large \sum\limits_{i=0}^\infty p^ix^i=\dfrac{1}{1-px}$
- $\large \sum\limits_{i=0}^\infty\dbinom{n-1+i}{i}p^ix^i=\dfrac{1}{(1-px)^n}$
- $\large \sum\limits_{i=0}^\infty\dbinom{n-1+i}{i}x^i=\dfrac{1}{(1-x)^n}$
- $\large \sum\limits_{i=0}^\infty x^{ik}=\dfrac{1}{1-x^k}$
求解生成函数的封闭形式
先看看六道例题。
六道例题
-
求解序列 $\langle0,1,1,\cdots\rangle$ 的生成函数的形式幂级数形式和封闭形式。
答案与解析
$G(x)=\sum\limits_{i=1}^\infty x^n=\dfrac{x}{1-x}$。
解析:
首先形式幂级数形式的生成函数很好求,然后发现当 $i=0$ 的时候对答案没有贡献,因此在 $\sum$ 中从 $1$ 开始累加。
考虑到上文提及的 $\large \sum\limits_{i=0}^\infty x^i=\dfrac{1}{1-x}$,那么便不难发现:
$$ \dfrac{G(x)}{x}=\sum\limits_{i=0}^\infty x^i=\dfrac{1}{1-x} $$
可以解得 $G(x)=\dfrac{x}{1-x}$。
其他方法列方程也可以,方法很多。
-
求解序列 $\langle1,0,1,0,1,\cdots\rangle$ 的生成函数的形式幂级数形式和封闭形式。
答案与解析
先说下我自己的方法。
显然 $G(x)=1+x^2+x^4+\cdots$,那么 $x\cdot G(x)=x+x^3+x^5+\cdots$。
因此:
$$ G(x)+x\cdot G(x)=1+x^2+x^3+\cdots=\sum\limits_{i=0}^\infty x^i=\dfrac{1}{1-x} $$
解得:
$$ G(x)=\dfrac{1}{(1+x)(1-x)}=\dfrac{1}{1-x^2} $$
再说说 OI Wiki 的方法。
考虑到:
$$ \begin{aligned} G(x)&=\sum_{n=0}^\infty x^{2n}\\ &=\sum_{n=0}^\infty \left(x^2\right)^n\\ &=\sum_{n=0}^\infty x^nx^n\\ &=\frac{1}{1-x^2} \end{aligned} $$
利用的是第 $3$ 个。
方法其实还有很多,比如利用等比数列。
-
求解序列 $\langle1,2,3,4,\cdots\rangle$ 的生成函数的形式幂级数形式和封闭形式。
答案与解析
显然:
$$ G(x)=\sum_{n=0}^\infty (n+1)x^n $$
即上文第 $2$ 个。
$$ G(x)=\frac{1}{(1-x)^2} $$
-
求解序列 $a_n=\dbinom{m}{n}$ 的生成函数($m$ 为常数)的形式幂级数形式和封闭形式。
答案与解析
$$ \begin{aligned} G(x)&=\sum_{n=0}^\infty\binom{m}{n}x^n\\ &=\sum_{n=0}^\infty\binom{m}{n}x^n1^{n-i}\\ &=(1+x)^m \end{aligned} $$
通过二项式定理可得。
-
求解序列 $a_n=\dbinom{m+n}{n}$ 的生成函数($m$ 为常数)的形式幂级数形式和封闭形式。
答案与解析
代入第 $4$ 个公式:
$$ \begin{aligned} G(x)&=\sum_{n=0}^\infty \binom{m+n}{n}x^n\\ &=\sum_{n=0}^\infty \binom{(m+1)-1+n}{n}\times 1^nx^n\\ &=\frac{1}{(1-1x)^{m+1}}\\ &=\frac{1}{(1-x)^{m+1}}\\ \end{aligned} $$
总结
主要是这几种方法:
- 列方程求解,多用于等比序列或者循环序列。
- 转换为已知封闭形式生成函数的形式幂级数形式后求解。
- 从递推式求解,见下文。
需要注意的是,无限序列 $a$ 中,若其生成函数为 $G(x)$ 且 $a_0,x>0$,则 $G(x)> x\cdot G(x)$。
通过求导求解生成函数的封闭形式
如果你不会求导可以看看。
事实上,此处的“求导”与其定义没有什么关系,仅仅是作为一种形式运算而存在,用于将生成函数变形。
对等式两侧进行求导来得到结果。
已知:
\[\sum\limits_{n=0}^\infty nx^n=\frac{x}{(1-x)^2}\]等式两边求导可得:
\[\sum_{n=1}^\infty n^2x^{n-1}=\frac{(1-x)^2-2x(1-x)(-1)}{(1-x)^4}\]化简:
\[\sum_{n=0}^\infty n^2x^{n-1}=\frac{1+x}{(1-x)^3}\]因此对于生成函数 $G(x)=\large \sum\limits_{\normalsize n=0}^{\normalsize \infty}\normalsize n^2x^n$ 就有:
\[\begin{aligned} G(x)&=\sum\limits_{n=0}^{\infty}n^2x^n\\ &=x\cdot \sum_{n=0}^\infty n^2x^{n-1}\\ &=\frac{x(1+x)}{(1-x)^3} \end{aligned}\]使用这种形式大多是为了将已知的生成函数 $G(x)$ 所有项的系数升次。
从递推式求解生成函数的封闭形式
在这种情况下求出的生成函数可能不存在形式幂级数形式。
根据递推式得出方程
Fibonacci 数列
以 Fibonacci 数列为例,通过递推式求解出其生成函数封闭形式。
规定:$f_0=0,f_1=1$,当 $n\geq 2$ 时有 $\large f_n=f_{n-1}+f_{n-2}$。
令其生成函数为:
\[\large F(x)=\sum_{n=0}^\infty f_nx^n\]原来的递推式可更改为:
\[f_n=\sum_{i=1}^kp_if_{n-i}\]其中,$k\leq n$。$k$ 表示 $\large f_{n-k},f_{n-k+1},f_{n-k+2},\cdots,f_{n-1}$ 与 $f_n$ 有关,$p_i$ 是系数,依递推式而定。
类似于“$x$ 进制”,显然 $F(x)$ 乘上一个 $x$ 就会“右移一位”,空出最左边的 $x^0$ 的位置;但是对于无限序列,考虑到其长度为无限,因此当 $a_0>0$ 时 $x\cdot F(x)$ 反而可能小于 $F(x)$,因为少了 $x_0$ 的位置。
因此我们可以修改上面的递推式,可得:
\[F(x)=\sum_{i=1}^kp_ix^iF(x)+G(x)\]其中,$G(x)$ 用于补齐 $k$ 位,其次数小于 $k$。
因为在 $n<k$ 时,递推式并不正确。
因此我们需要使用 $G(x)$ 来使这一“边界情况”保持正确。
进一步变换得到:
\[F(x)=\frac{G(x)}{1-\sum\limits_{i=1}^kp_ix^i}\]显然,这个例子不太例子。
代入 $k=2,p_1=p_2=1$ 得:
\[\begin{aligned} F(x)&=x\cdot F(x)+x^2\cdot F(x)+G(x)\\ &=(x^2+x)F(x)+G(x) \end{aligned}\]这时,我们用于补全的 $G(x)$ 为 $x$(根据不同的定义,也有可能为 $1$)。
因为 $F(x)=(x^2+x)F(x)$ 递推的时候并没有递推 $f_0\sim f_{k-1}$ 的值,因此需要手动加上这个值,否则 $f_1$ 没有值。$f_0$ 为 $0$ 不需要加。
则:
\[F(x)=\frac{x}{1-x-x^2}\]但是这样似乎就会出现一个问题:若 $f_i$ 的值不仅仅与 $f_j$ 有关呢?
考虑与 $f_i$ 有关的数可能是哪些:常数,$f$ 的其他项 $f_j$,$i$。
事实上,如果 $f_i$ 与 $i$ 或常数有关,仍然可以求解。
$f_i$ 递推式包含 $i$ 和常数
例如:$f_0=0,f_1=1$,对于 $n\geq 2$ 有 $f_n=3f_{n-1}+2f_{n-2}+n-2$。(常数、$f$ 的其他项,$n$ 兼具)
定义其生成函数为:
\[F(x)=\sum_{n=0}^\infty f_nx^n\]若递推式为 $f_n=3f_{n-1}+2f_{n-2}$,可以很好得出($G(x)=x$):
\[F(x)=3x\cdot F(x)+2x^2\cdot F(x)+x\]然而,$n-2$ 似乎不知道如何处理。
事实上,我们 $n-2$ 也可以构造出一个序列 $a=\left\langle\triangle,\triangle,0,1,2,\cdots\right\rangle$ 满足递推式 $a_n=a_{n-1}+1,a_2=0$。($\triangle$ 表示不存在)
那么序列 $a$ 的生成函数为:
\[\begin{aligned} A(x)&=\sum_{i=2}^\infty a_ix^i\\ &=\sum_{i=2}^\infty(i-2)x^i\\ &=\sum_{i=0}^{\infty}ix^{i+2}\\ &=\sum_{i=1}^\infty ix^{i+2}\\ &=\sum_{i=0}^\infty (i+1)x^{i+3}\\ &=x^3\sum_{i=0}^\infty (i+1)x^i\\ &=\frac{x^3}{(1-x)^2}\\ \end{aligned}\]那么我们用刚才求出的 $F(x)$ 加上 $A(x)$ 即序列 $f$ 的生成函数。
即:
\[\begin{aligned} F(x)&=3x\cdot F(x)+2x^2\cdot F(x)+A(x)+G(x)\\ (1-3x-2x^2)F(x)&=\frac{x^3}{(1-x)^2}+x\\ F(x)&=\dfrac{\dfrac{x^3}{(1-x)^2}+x}{1-3x-2x^2}\\ \end{aligned}\]$f_i$ 递推式中包含 $f_j$ 项的次数不为 $1$(Catalan 数)
例如:对于序列 $f$,满足 $f_0=1,f_n=\sum\limits_{i=0}^{n-1}f_if_{n-i-1}$,求其生成函数 $F(x)$ 的封闭形式。其实就是卡特兰数。
首先对于 $\large \sum\limits_{i=0}^{n-1}f_if_{n-i-1}$,明显可看作是一个类似于“卷积后上升一位”的形式。
因此我们就可以得到:
\[\begin{aligned} F(x)&=\sum_{n=0}^\infty f_nx^n\\ &=xF^2(x)+G(x)\\ &=x\cdot F^2(x)+1\\ \end{aligned}\]解得:
\[F(x)=\frac{1\pm \sqrt{1-4x}}{2x}\]但是很明显,$F(x)$ 只可能对应一个封闭形式,因此必然需要舍弃一个根。
考虑到如果是 $\dfrac{1+\sqrt{1-4x}}{2x}$,则不能够消除 $\dfrac{1}{2x}$ 的 $1$ 的常数项,因此根为 $\dfrac{1-\sqrt{1-4x}}{2x}$。
故,$F(x)$ 的封闭形式为: \(F(x)=\frac{1-\sqrt{1-4x}}{2x}\)
总结
可以根据序列 $f$ 的递推式得出方程进而求解。
如果是 $f_{n-i}$,那么在生成函数 $F(x)$ 中的对应项就是 $x^i\cdot F(x)$。
对于一般的一次递推式存在通法(二次递推式一般需要去根,一次不需要):
对于序列 $f$ 满足:
\[f_i= \begin{cases} g_i&i<k\\ \sum\limits_{n=1}^kp_nf_{n-i}+a_i&i\geq k \end{cases}\]其生成函数 $F(x)$ 为:
\[F(x)=\frac{A(x)+G(x)}{1-\sum\limits_{i=1}^kp_ix^i}\]其中,$A(x)$ 是序列 $a$ 的生成函数,$G(x)$ 是有限序列 $g$ 的生成函数,满足 $\vert g\vert\leq k$。
从生成函数的封闭形式求解通项公式
Fibonacci 数列通项公式
已知 Fibonacci 数列满足 $f_0=0,f_1=1,f_n=f_{n-1}+f_{n-2}$,其生成函数为 $F(x)=\dfrac{x}{1-x-x^2}$。
令:
\[\begin{aligned} \frac{x}{1-x-x^2}&=\frac{A}{1-ax}+\frac{B}{1-bx}\\ &=\frac{(A-Abx)+(B-Bax)}{(1-ax)(1-bx)}\\ &=\frac{(A+B)-(Ab+Ba)x}{1-(a+b)x+ab\cdot x^2}\\ \end{aligned}\]则可列:
\[\begin{cases} A+B=0\\ -(Ab+Ba)=1\\ a+b=1\\ ab=-1\\ \end{cases}\]解得:
\[\begin{cases} A=\dfrac1{\sqrt5}\\ B=-\dfrac1{\sqrt5}\\ a=\dfrac{1+\sqrt5}2\\ b=\dfrac{1-\sqrt5}{2}\\ \end{cases}\]所谓“通项公式”,其实就是生成函数中 $x^n$ 项的系数。
因此我们需要将生成函数 $F(x)$ 转换为形式幂级数形式。
考虑将 $\dfrac{A}{1-ax},\dfrac{B}{1-bx}$ 转换为形式幂级数形式:
\[\begin{aligned} \frac{A}{1-ax}&=A\cdot \frac{1}{1-ax}\\ &=A\sum_{n=0}^\infty a^nx^n \end{aligned}\]同理,$\dfrac{B}{1-bx}=B{\Large \sum\limits_{\normalsize n=0}^{\normalsize\infty}} b^nx^n$。
则:
\[\begin{aligned} F(x)&=\frac{a}{1-ax}+\frac{b}{1-bx}\\ &=A\sum_{n=0}^\infty a^nx^n+B\sum_{n=0}^\infty b^nx^n\\ &=\sum_{n=0}^\infty\left(A\cdot a^n+B\cdot b^n\right)x^n \end{aligned}\]代入 $A,B,a,b$ 的值,可得:
\[F(x)=\sum_{n=0}^\infty \frac{1}{\sqrt5}\left[\left(\frac{1+\sqrt5}{2}\right)^n-\left(\frac{1-\sqrt5}{2}\right)^n\right] x^n\]则,通项公式为:
\[f_n=\frac{1}{\sqrt5}\left[\left(\frac{1+\sqrt5}{2}\right)^n-\left(\frac{1-\sqrt5}{2}\right)^n\right]\]总结
- 求出生成函数封闭形式。
- 通过待定系数法列方程,将原本的封闭形式划分为若干个部分。
- 将若干个部分转换为形式幂级数形式。
- 合并答案。
其实就是一个减小规模的过程,因为直接转换初始的 $F(x)$ 不那么简单。
指数生成函数
指数生成函数用于处理排列问题。
定义序列 $a_1,a_2,a_3,\cdots,a_n,\cdots$ 的指数生成函数为形式幂级数:
\[G(x)=\sum_{n=0}^\infty a_n\cdot\frac{x^n}{n!}\]由于很多部分都是与普通生成函数类似的,故不再做解释。此部分仅解释不同之处。
阶乘分母
对于 $G(x)$ 中的 $\dfrac{x^n}{n!}$,其表示的是某个元素出现了 $n$ 次。
但是,在不同位置出现的会重复计算,因此应当除以 $n!$。
$e^x$ 的泰勒展开式
在高等数学中,对于 $e^x$ 有:
\[\begin{aligned} e^x&=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots+\frac{x^n}{n!}+\cdots\\ &=\sum_{n=0}^\infty\frac{x^n}{n!} \end{aligned}\]对于 $e^{-x}$ 有:
\[\begin{aligned} e^{-x}&=1-\frac{x}{1!}+\frac{x^2}{2!}-\frac{x^3}{3!}+\cdots+\frac{x^n}{n!}-\frac{x^{n+1}}{(n+1)!}+\cdots\\ &=\sum_{n=0}^\infty\frac{(-x)^n}{n!} \end{aligned}\]可以很明显的发现,这与指数生成函数存在相似之处。
事实上,这也是其命名的由来。
还有:
\[\begin{aligned} 1+\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots&=\frac{e^x+e^{-x}}{2}\\ \frac{x}{1!}+\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots&=\frac{e^x-e^{-x}}{2} \end{aligned}\]在指数生成函数运算过程中,请牢记以上公式。
乘法运算
指数生成函数的乘法需要另行讨论。
对于两个序列 $\langle a_1,a_2,a_3,\cdots,a_n,\cdots\rangle,\langle b_1,b_2,b_3,\cdots,b_n,\cdots\rangle$,设其指数生成函数分别为 $A(x),B(x)$。
则:
\[A(x)\cdot B(x)=\sum_{i=0}^\infty a_i\cdot\frac{x^i}{i!}\sum_{j=0}^\infty b_j\cdot\frac{x^j}{j!}\]同普通生成函数的多项式卷积,这也无法计算,于是令 $n=i+j$。
则:
\[\begin{aligned} A(x)\cdot B(x)&=\sum_{n=0}^\infty\sum_{i=0}^n\left(a_i\cdot\frac{x^i}{i!}\right)\left(b_{n-i}\cdot\frac{x^{n-i}}{(n-i)!}\right)\\ &=\sum_{n=0}^\infty\sum_{i=0}^na_ib_{n-i}\cdot\frac{x^n}{i!(n-i)!}\\ &=\sum_{n=0}^\infty\frac{x^n}{n!}\sum_{i=0}^na_ib_{n-i}\cdot\frac{n!}{i!(n-i)!}\\ &=\sum_{n=0}^\infty\left(\sum_{i=0}^n\binom{n}{i}a_ib_{n-i}\right)\frac{x^n}{n!}\\ \end{aligned}\]因此,$A(x)\cdot B(x)$ 是序列 $\left\langle\sum\limits_{i=0}^n\binom{n}{i}a_ib_{n-i}\right\rangle$ 的指数生成函数。
一道例题
求 $1,3,5,7,9$ 这五个数字组成的 $n$ 位数的个数,要求其中 $3,7$ 出现的次数为偶数,其它数字出现的次数不加限制。
定义函数 $G_1(x),G_3(x),G_5(x),G_7(x),G_9(x)$,分别表示其出现次数序列的指数生成函数。
对于 $3,7$ 只能出现偶数次,有:
\[\begin{aligned} G_3(x)=G_7(x)&=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\frac{x^6}{6!}+\cdots\\ &=\frac{e^x+e^{-x}}{2} \end{aligned}\]对于 $1,5,9$,有:
\[\begin{aligned} G_1(x)=G_5(x)=G_9(x)&=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots\\ &=e^x \end{aligned}\]设满足条件的 $n$ 位数的个数为 $a_n$,则 $\langle a_n\rangle$ 的指数生成函数为 $G(x)$。
则:
\[\begin{aligned} G(x)&=G_1(x)\cdot G_3(x)\cdot G_5(x)\cdot G_7(x)\cdot G_9(x)\\ &=\left(e^x\right)^3\left(\frac{e^x+e^{-x}}{2}\right)^2\\ &=e^{3x}\cdot\frac{e^{2x}+2+e^{-2x}}{4}\\ &=\frac{e^{5x}+2e^{3x}+e^x}{4} \end{aligned}\]考虑到:
\[\begin{cases} \begin{aligned} e^{5x}&=\sum_{n=0}^\infty\frac{(5x)^n}{n!}\\ &=\sum_{n=0}^\infty\frac{5^nx^n}{n!}\\ e^{3x}&=\sum_{n=0}^\infty\frac{(3x)^n}{n!}\\ &=\sum_{n=0}^\infty\frac{3^nx^n}{n!}\\ e^x&=\sum_{n=0}^\infty\frac{x^n}{n!}\\ \end{aligned} \end{cases}\]代入原式:
\[\begin{aligned} G(x)&=\dfrac{\large \sum\limits_{\normalsize n=0}^{\normalsize \infty}\normalsize\dfrac{5^nx^n}{n!} + 2\large \sum\limits_{\normalsize n=0}^{\normalsize \infty}\normalsize\dfrac{3^nx^n}{n!} + \large \sum\limits_{\normalsize n=0}^{\normalsize \infty}\normalsize\dfrac{x^n}{n!}}{4}\\ &=\dfrac{\large\sum\limits_{\normalsize n=0}^{\normalsize\infty}\normalsize\dfrac{\left(5^n+2\times3^n+1\right)x^n}{n!}}{4}\\ &=\sum_{n=0}^\infty\left(\frac{5^n+2\times3^n+1}{4n!}\right)x^n \end{aligned}\]则答案 $a_n=\dfrac{5^n+2\times 3^n+1}{4n!}$。
总结
-
指数生成函数运算时,需要牢记 $e^x$ 与形式幂级数之间的转换关系。
- 乘法运算相比普通生成函数多了一个组合数。
- 需要注意什么时候(排列问题)应当使用指数生成函数。
多项式系数
已知多项式 $\left(\sum\limits_{i=1}^ma_i\right)^n$ 的展开式,则其 $a_1^{n_1}a_2^{n_2}a_3^{n_3}\cdots a_{m}^{n_m}$ 项的系数为:
\[\binom{n}{n_1}\binom{n-n_1}{n_2}\binom{n-n_1-n_2}{n_3}\cdots\binom{n-n_1-n_2-\cdots-n_{m-1}}{n_m}=\dfrac{n!}{n_1!n_2!n_3!\cdots n_m!}\]分拆数
将一个正整数 $n$ 分为若干个个正整数相加,即令 $n$ 表示为 $n=a_1+a_2+a_3+\cdots+a_k$,满足 $a_i\geq1$。
交换 $a_i,a_j$ 的顺序不影响答案(这是一个组合问题),因此为了便于分析不妨令 $a_1\geq a_2\geq a_3\geq\cdots\geq a_k$。
$k$ 部分分拆数
将 $n$ 划分为 $k$ 个部分的分拆数,称为“$k$ 部分分拆数”,方案数记作 $p(n,k)$。
则:
\[p_n=\sum_{k=1}^np(n,k)\]解法一
这是教的时候教的做法,也是资料上的。
显然,$p(n,k)$ 即下列方程的非负整数解组的个数:
\(n-k=b_1+b_2+b_3+\cdots+b_k\) 满足 $b_1\geq b_2\geq b_3\geq \cdots\geq b_k\geq 0$。
假设在 $b_1,b_2,b_3,\cdots,b_k$ 中,有 $m$ 个数大于 $0$。
即:
\[b_1\geq b_2\geq b_3\geq\cdots\geq b_{k'}>b_{k'+1}=b_{k'+2}=\cdots=b_k=0\]因此有和式:
\[p(n,k)=\sum_{m=0}^k p(n-k,m)\]解释:$n-k$ 代表给 $k$ 个部分都预先分配一个 $1$ 防止$a_i=0$,随后将其划分为 $m$ 个大于 $0$ 的部分即可。
相邻两个和式作差,化简得:
\(p(n,k)=p(n-1,k-1)+p(n-k,k)\)
虽然我并不知道如何化简。
解法二
自己想的。
考虑将 $n$ 划分为 $k$ 个部分时,最小部分可能的取值。
- 取 $1$。
- 取 $2$ 以上的正整数。
如果是第一种情况,方案数为 $p(n-1,k-1)$,即将 $n-1$ 划分为 $k-1$ 个部分,再加上这个 $1$。
否则对于第二种情况,先给每一个部分都分配一个 $1$ 防止出现 $0$,然后将 $n-k$ 划分为 $k$ 个部分再加上即可。
即:
\[p(n,k)=p(n-1,k-1)+p(n-k,k)\]注意此处之所以不是 $p(n-k,k-1)$ 而是 $p(n-1,j-1)$,是因为只考虑第 $k$ 项的取值,前面的会在递归或递推中考虑,不然会重复计数。
解法三
存在一种 $\mathcal O\left(n\sqrt n\right)$ 的解法,参见参考资料。
生成函数
注意:所有分拆数的生成函数的起始位置都是 $1$,而不是 $0$,因为不能划分为 $0$ 个部分。
令 $p_n$ 表示正整数 $n$ 的分拆数目。
则:
\[p_n=\sum_{i=1}^n p(n,i)\]那么,分拆数数目 $p_n$ 的生成函数为:
\[\begin{aligned} G(x)&=1+p_1x+p_2x^2+p_3x^3+\cdots\\ &=\frac{1}{1-x}\cdot\frac{1}{1-x^2}\cdot\frac{1}{1-x^3}\cdot\cdots \end{aligned}\]至多划分为 $k$ 个部分的数目为: \(\left[x^n\right]G(x)=\frac{1}{(1-x)(1-x^2)\cdots(1-x^k)}\) 恰好划分为 $k$ 个部分的数目为: \(\left[x^n\right]G(x)=\frac{x^k}{(1-x)(1-x^2)\cdots(1-x^k)}\) $k$ 部分分拆数 $p(n,k)$ 的生成函数为:
\[\sum_{n,k\geq0}p(n,k)x^ny^k=\prod_{i=1}^\infty\frac{1}{1-x^iy}\]Ferrers 图
所谓 Ferrers 图,其实就是将分拆数分拆出的每一个部分都用一行若干个点表示。
具体而言,将整数 $n$ 拆分为 $k$ 个部分 $a_1,a_2,a_3,\cdots,a_k$,则对应的 Ferrers 图中第一行有 $a_1$ 个点,第二行有 $a_2$ 个点,第三行有 $a_3$ 个点……第 $k$ 行有 $a_k$ 个点。
比如:将 $12$ 分拆为 $12=5+4+2+1$,$n=12,k=4$
将其沿主对角线(左上至右下)翻转:
可以发现,这就等同于将 $12$ 分拆为了 $12=4+3+2+2+1$。
而第一行对应原图中的第一列,考虑到分拆数不能拆出 $0$,因此原图中的 $k$ 行每行都是存在的,那么新图中第一行(也是最长的一行)的长度就是 $k$。
即:新图对应的分拆方案中最大的部分为 $k$。
也就是说,$k$ 部分分拆数等同于最大 $k$ 分拆数,均为 $p(n,k)$。
最大 $k$ 分拆数
等同于 $k$ 部分分拆数。
互异分拆数
令 $pd_n$ 表示 $n$ 个各部分互不相同的分拆方案数。
$k$ 部分互异分拆数
将 $n$ 划分为 $k$ 个互不相同的部分的分拆数,称为“$k$ 部分互异分拆数”,方案数记作 $pd(n,k)$。
则:
\[pd_n=\sum_{k=1}^npd(n,k)\]解法一
同上文解法一,$pd(n,k)$ 即下列方程的非负整数解的个数: \(n-k=b_1+b_2+b_3+\cdots+b_k\) 满足 $b_1>b_2>b_3>\cdots>b_k\geq 0$。
则只有 $b_k$ 可能取 $0$。
当 $b_k=0$ 时,方案数为 $pd(n-k,k-1)$。
否则,方案数为 $pd(n-k,k)$。
即:
\[pd(n,k)=pd(n-k,k-1)+pd(n-k,k)\]伪·解法二
其实和上面那一种一样……
本部分仅仅是为了解释为什么不同上文解法二一样思考、递推,自己推一下就能发现。
生成函数
互异分拆数的生成函数为:
\[\prod_{i=1}^\infty\left(x^0+x^i\right)=\prod_{i=1}^\infty\left(1+x^i\right)\]对于每一个正整数 $i$,都存在两种选择:包含在方案中($x^i$)和不包含在方案中($x^0$)。
奇分拆数
令 $po_n$ 表示将 $n$ 拆分为若干个部分,且各部分均为奇数的分拆方案数。
生成函数
奇分拆数的生成函数为:
\[\prod_{k=1}^\infty\sum_{i=0}^\infty x^{i(2k-1)}=\prod_{k=1}^\infty\frac{1}{1-x^{2k-1}}\]因为对于每一个奇数 $2k-1$,都可能出现在分拆中 $i$ 次。
等价问题
考虑到:
\[\prod_{i=1}^\infty\left(1+x^i\right)=\frac{\prod\limits_{i=1}^\infty\left(1-x^{2i}\right)}{\prod\limits_{i=1}^\infty\left(1-x^i\right)}=\prod_{i=1}^\infty\frac{1}{1-x^{2i-1}}\]最左侧是互异分拆数的生成函数,最右侧即奇拆分数的生成函数。
那么:$po_n=pd_n$。
由于 $k$ 部分奇分拆数过于复杂基本用不上且我不会,不予展示。
Fibonacci 数列 斐波那契数列
定义
最规范的定义是 $f_0=0,f_1=1$,当 $n\geq2$ 时 $f_n=f_{n-1}+f_{n-2}$,此处也采用这种。
否则会在一些细节上不同。
通项公式
\[f_n=\frac{1}{\sqrt5}\left[\left(\frac{1+\sqrt5}{2}\right)^n-\left(\frac{1-\sqrt5}{2}\right)^n\right]\]推导见此处。
当然,不难发现 $\dfrac{1-\sqrt5}{2}<0$,那么在公式中就是以指数级的速度减小。
记 $[x]$ 表示离 $x$ 最近的整数。
则:
\[f_n=\left[\frac{\left(\frac{1+\sqrt5}{2}\right)^n}{\sqrt5}\right]\]性质
- 卡西尼性质:$f_{n-1}f_{n+1}-f_n^2=(-1)^n$。
- 附加性质:$f_{n+k}=f_kf_{n+1}+f_{k-1}n$。
- 取第二条性质中 $k=n$,则 $f_{2n}=f_nf_{n+1}+f_{n-1}f_n$。
- 由第三条性质归纳可得,$\forall k\in\N,f_n\mid f_{nk}$。
- 第四条性质可逆,即 $\forall f_a\mid f_b,a\mid b$。
- $\gcd(f_m,f_n)=f_{\gcd(m,n)}$。
- 以 $f_i,f_{i+1}$ 为输入会使欧几里得算法的复杂度达到最坏情况(具体参见维基 - 拉梅)。
其实可以推广到一些线性递推数列。对于一个序列 $f_n=af_{n-1}+bf_{n-2}$,若 $\gcd(a,b)=1,f_0=0,f_1=1$,则有:
\[\gcd(f_i,f_j)=f_{\gcd(i,j)}\]证明
构造转移矩阵:
$$ \begin{bmatrix} a&b\\ 1&0 \end{bmatrix} \begin{bmatrix} f_n\\ f_{n-1} \end{bmatrix} = \begin{bmatrix} f_{n+1}\\ f_n \end{bmatrix} $$
不妨令 $i<j$,则有:
$$ \begin{aligned} \begin{bmatrix} a&b\\ 1&0 \end{bmatrix}^{j-i} \begin{bmatrix} f_i\\ f_{i-1} \end{bmatrix} &= \begin{bmatrix} f_{j+1}\\ f_j \end{bmatrix} \\ \begin{bmatrix} f_{j-i+2}&f_{j-i+1}\\ f_{j-i+1}&f_{j-i}\\ \end{bmatrix} \begin{bmatrix} f_i\\ f_{i-1} \end{bmatrix} &= \begin{bmatrix} f_{j+1}\\ f_j \end{bmatrix} \end{aligned} $$
注意到:
$$ f_j=f_{j-i+1}f_i+f_{j-i}f_{i-1} $$
则有:
$$ \gcd(f_i,f_j)=\gcd(f_i,f_{j-i}f_{i-1}) $$
数学归纳可得 $\gcd(f_i,f_{i-1})=1$,因此有:
$$ \gcd(f_i,f_j)=\gcd(f_i,f_{j-i}) $$
由辗转相减,最终得到:
$$ \gcd(f_i,f_j)=f_{\gcd(i,j)} $$
模意义下的周期性
考虑模 $P$ 意义下斐波那契数列的周期性。
考虑这样 $p^2+1$ 对斐波那契数:
\[(f_1,f_2),(f_2,f_3),\cdots,(f_{p^2+1},f_{p^2+2})\]由鸽巢原理,至少存在两对 $(f_a,f_{a+1}),(f_b,f_{b+1})$ 满足 $f_a=f_b,f_{a+1}=f_{b+1}$。
这样,生成的下一个数是相同的,因此模意义下斐波那契数列具有周期性。
皮萨诺周期
模 $p$ 意义下的斐波那契数列的最小正周期被称为皮萨诺周期,记作 $\pi(p)$,且:
\[\pi(p)\leq6p\]$\pi(p)=6p$ 成立当且仅当 $p=2\times5^r\land r>1$。
若 $p$ 不能表示为 $2\times5^r$ 的形式,则 $\pi(p)\leq4p$.
Stirling 数 斯特林数
为什么优先介绍第二类 Stirling 数
因为第二类 Stirling 数更常用,且在其本人的著作中也是优先介绍第二类 Stirling 数。
第二类 Stirling 数
第二类 Stirling 数表示的是将 $n$ 个不同的元素划分为 $k$ 个互不区分的非空子集的方案数,记为 \(\begin{Bmatrix}n\\k\end{Bmatrix}\),也可记作 $S(n,k)$。
第二类 Stirling 数的 $\KaTeX$ 输入
$\begin{Bmatrix}n\\k\end{Bmatrix}$ 的代码:
1
2
3
4
\begin{Bmatrix}
n\\
k
\end{Bmatrix}
递推式
在划分一个新元素时,存在两种情况:
- 将新元素单独划分,方案数:\(\begin{Bmatrix}n-1\\k-1\end{Bmatrix}\)。
- 放入现有的 $k$ 个子集,方案数:\(k\begin{Bmatrix}n-1\\k\end{Bmatrix}\)。
则总方案数为:
\[\begin{Bmatrix} n\\ k \end{Bmatrix} = \begin{Bmatrix} n-1\\ k-1 \end{Bmatrix} + k \begin{Bmatrix} n-1\\ k \end{Bmatrix}\]边界:
\[\begin{Bmatrix} n\\ 0 \end{Bmatrix} =[n=0]\]通项公式
\[\begin{Bmatrix}n\\k\end{Bmatrix}=\sum_{i=0}^k\frac{(-1)^{k-i}i^n}{i!(k-i)!}\]证明:参见OI Wiki。
同一行的第二类 Stirling 数计算
即 $n$ 确定,求 \(\begin{Bmatrix}n\\0\end{Bmatrix},\begin{Bmatrix}n\\1\end{Bmatrix},\begin{Bmatrix}n\\2\end{Bmatrix},\cdots\) 的值。
根据通项公式卷积计算即可。
时间复杂度:$\mathcal O(n\log n)$。
同一列的第二类 Stirling 数计算
即 $k$ 确定,求 \(\begin{Bmatrix}0\\k\end{Bmatrix},\begin{Bmatrix}1\\k\end{Bmatrix},\begin{Bmatrix}2\\k\end{Bmatrix},\cdots\) 的值。
参见OI Wiki。
不会。
第一类 Stirling 数
又称“Sitrling 轮换数”或“斯特林轮换数”,表示将 $n$ 个不同的元素划分为 $k$ 个互不区分的非空轮换的方案数,记作 \(\begin{bmatrix}n\\k\end{bmatrix}\),也可记作 $s(n,k)$。
轮换的定义
一个轮换即一个首尾相接的圆排列,能够通过旋转而互相转换的轮换等价。
即:若 $[a,b,c,d]$ 是一个轮换,则:
$$ [a,b,c,d]=[b,c,d,a]=[c,d,a,b]=[d,a,b,c] $$
递推式
与第二类 Stirling 数类似,在划分一个新元素时,同样有两种情况:
-
划分至一个新的非空轮换,方案数为 \(\begin{bmatrix}n-1\\k-1\end{bmatrix}\)。
-
划分至现有轮换,方案数为 \((n-1)\begin{bmatrix}n-1\\k\end{bmatrix}\)。
则总方案数为:
\[\begin{bmatrix} n\\k \end{bmatrix} = \begin{bmatrix} n-1\\k-1 \end{bmatrix} +(n-1) \begin{bmatrix} n-1\\k \end{bmatrix}\]不存在实用通项公式
第一类 Stirling 数不存在实用的通项公式。
同一行的第一类 Stirling 数计算
参见OI Wiki。
不会。
同一列的第一类 Stirling 数计算
参见OI Wiki。
不会。
普通幂与上升幂
所谓上升幂,即记 $x^{\overline{n}}$ 表示:
\[x^{\overline{n}}=\prod_{i=0}^{n-1}(x+i)=x(x+1)(x+2)\cdots(x+n-1)\]则有:
\[\begin{aligned} x^{\overline{n}}&=\sum_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}x^k\\ x^n&=\sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}(-1)^{n-k}x^{\overline k} \end{aligned}\]普通幂与下降幂
所谓下降幂,即记 $x^{\underline n}$ 表示:
\[x^{\underline{n}}=\prod_{i=0}^{n-1}(x-i)=x(x-1)(x-2)\cdots(x-n+1)=P^{n}_{x}=\dbinom{x}{n}n!\]则有:
\[\begin{aligned} x^{\underline{n}}&=\sum_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}(-1)^{n-k}x^k\\ x^n&=\sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}x^{\underline{k}}\\ &=\sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}k!\dbinom{n}{k} \end{aligned}\]Catalan 数 卡特兰数
Catalan 数是一个定义的数列,可以用于求解一些问题,例如:
- 对角线不相交的情况下,将一个凸多边形区域分成三角形区域的方法数。
- 在一个大小为 $n\times n$ 的方格图的左下角走到右上角,每次只能向右或向上一个单位,不走到对角线 $y=x$ 上方(但可以触碰)的方案数。
- 已知一个栈的入栈序列为 $a_1,a_2,a_3,\cdots,a_n$,求其可能的出栈序列的数目。
- $n$ 个节点构成的不同的二叉树的数目。([TJOI2015] 概率论)
- 更多参见OI Wiki。
满足边界条件 $f_0=1$。
递推式
Catalan 数的递推式为:
\[f_n=\sum_{i=0}^{n-1}f_if_{n-i-1}\]接下来从两个问题的角度分析 Catalan 数的应用。
将一个凸多边形区域分成三角形区域的方法数
如图,取 $n=7$:
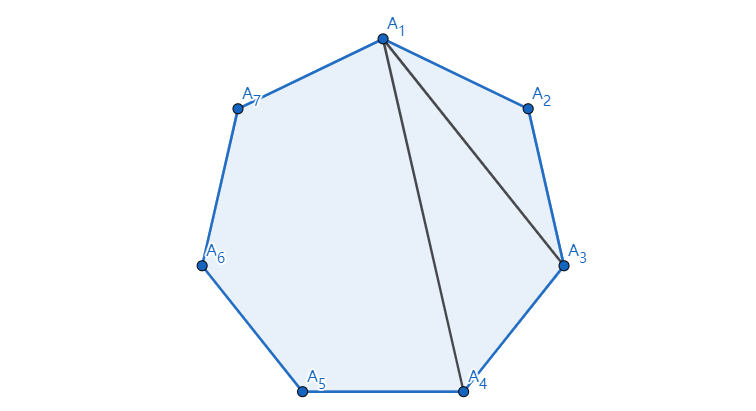
对于 $n$ 边形 $A_1A_2A_3\cdots A_n$,可以找到两点 $A_k,A_{k+1}$,从而使得 $A_1A_kA_{k+1}$ 构成三角形。图中取 $k=3$。
而原图也被 $\triangle A_1A_kA_{k+1}$ 划分为了两部分:$k$ 边形 $A_1A_2\cdots A_k$ 和 $n-k-1$ 边形 $A_{k+1}A_{k+2}A_{k+3}\cdots A_nA_1$。
令 $f_m$ 表示 $m$ 边形的划分方案。
则取 $k=3$ 时的方案即为 $f_kf_{n-k-1}$。
枚举 $k$ 后取和即可。即 Catalan 数。
格路问题 路径计数问题
见格路问题部分。
出栈序列数目
已知入栈序列 $a_1,a_2,a_3,\cdots,a_n$。
令 $f_{i,j}$ 表示当前 $i$ 个元素尚未入过栈,栈中尚有 $j$ 个元素时的方案数。
则答案为 $f_{n,0}$。
显然有:
- $f_{0,j}=1$,因为此时只能出栈。
- $f_{i,-1}=0$,因为此情况不存在。
- 否则,$f_{i,j}=f_{i,j-1}+f_{i-1,j+1}$。
生成函数
封闭形式见上文“从递推式求解生成函数的封闭形式”。
形式幂级数形式的的推导过程推导见OI Wiki。
其为:
\[f_n=\frac{1}{n+1}\binom{2n}{n}\]贝尔数
记 $B_n$ 为将 $n$ 个互不相同的元素划分为若干个互不区分的集合的方案数。
则有:
\[B_{n+1}=\sum_{k=1}^n\binom{n}{k}B_k\]同时满足:
\[B_n=\sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}\]贝尔数本身其实没什么意义,但是注意到 $B_{13}=27644437,B_{14}=190899322$,因此在此类问题中,搜索的复杂度可以接受到 $n=14$。
容斥原理与鸽巢原理
容斥原理 抽屉原则
引入例题
已知:$\vert A\vert=12,\vert B\vert=8,\vert C\vert=5,\left\vert A\bigcap B\right\vert=3,\left\vert B\bigcap C\right\vert=4,\vert A\bigcap C\vert=9,\vert A\bigcup B\bigcup C\vert=20$。
求:$\vert A\bigcap B\bigcap C\vert$。
这就是很明显的容斥原理。
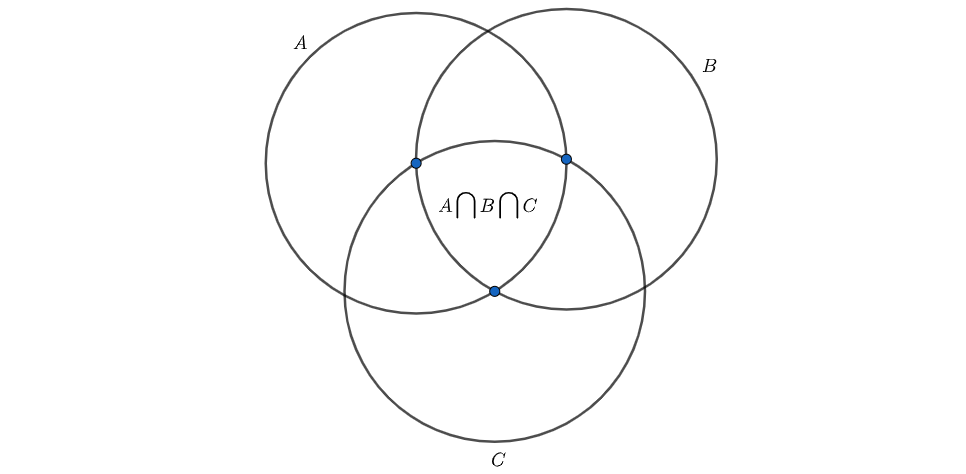
答案即:
\[\begin{aligned} \vert A\small\bigcup\normalsize B\small\bigcup\normalsize C\vert-\vert A\vert-\vert B\vert-\vert C\vert+\vert A\small\bigcap\normalsize B\vert+\vert B\small\bigcap\normalsize C\vert+\vert A\small\bigcap\normalsize C\vert&=20-12-8-5+3+4+9\\ &=11 \end{aligned}\]基本原理
为了方便表述,一般会使用集合论的知识。
所谓容斥原理,其实就是用“总情况”减去“不符合条件的情况”得到“符合条件的情况”。
容斥原理就是对于集合 $S_i$,明确元的性质 $P_i$ 从而确定 $S_i$。
设总元素集合 $U$ 中存在 $n$ 种不同性质 $P_1,P_2,P_3,\cdots,P_n$,拥有性质 $P_i$ 的所有元素构成集合 $S_i$,则:
\[\begin{aligned} \left\vert\bigcup_{i=1}^nS_i\right\vert&=\sum_{1\leq i\leq n}\vert S_i\vert-\sum_{1\leq i<j\leq n}\vert S_i\bigcap S_j\vert+\sum_{1\leq i<j<k\leq n}\vert S_i\bigcap S_j\bigcap S_k\vert-\cdots+(-1)^{n-1}\left\vert\bigcap_{i=1}^n S_i\right\vert\\ &=\sum_{i=1}^n(-1)^{i-1}\sum_{1\leq a_1<a_2<\cdots<a_i\leq n}\left\vert\bigcap_{j=1}^iS_{a_j}\right\vert\\ \end{aligned}\]数学归纳法证明
当 $n=1$ 时,上式显然成立。
那么假定 $n=m$ 时成立,若能够证明 $n=m+1$ 时也成立,则原命题成立。
$n=m$ 时成立,即:
$$ \left\vert\bigcup_{i=1}^mS_i\right\vert=\sum_{1\leq i\leq m}\vert S_i\vert-\sum_{1\leq i<j\leq m}\vert S_i\bigcap S_j\vert+\sum_{1\leq i<j<k\leq m}\vert S_i\bigcap S_j\bigcap S_k\vert-\cdots+(-1)^{m-1}\left\vert\bigcap_{i=1}^m S_i\right\vert $$
令集合 $A=\bigcup\limits_{i=1}^mS_i$,则 $\bigcup\limits_{i=1}^{m+1}S_i=A\bigcup S_{m+1}$。
由容斥原理,有:
$$ A\bigcup S_{m+1}=\vert A\vert+\vert S_{m+1}\vert-\vert A\bigcap S_{m+1}\vert $$
展开交集大小 $\vert A\bigcap S_{m+1}\vert$ 得:
$$ \begin{aligned} \vert A\bigcap S_{m+1}\vert&=\sum_{1\leq i\leq m}\vert S_i\bigcap S_{m+1}\vert - \sum_{1\leq i<j\leq m}\vert S_i\bigcap S_j\bigcap S_{m+1} \vert+\cdots+(-1)^{m-1}\left\vert\bigcap_{i=1}^mS_i\bigcap S_{m+1}\right\vert \end{aligned} $$
回代,即可证明当 $n=m+1$ 时成立。
故,原命题成立。
二项式定理证明
观察等式,可以发现元素 $x$ 在左边显然只统计了 $1$ 次。
不妨设元素 $x$ 属于 $m$ 个集合。
由组合数,在右边出现的次数为:
$$ \begin{aligned} \sum\limits_{i=1}^m(-1)^{i-1}\dbinom{m}{i}&=\dbinom{m}{0}-\sum\limits_{i=0}^m(-1)^{i-1}\dbinom{m}{i}\\ &=1-(1-1)^m\\ &=1\\ \end{aligned} $$
可以发现,对于任意元素 $x$,在左右两边都只统计了一次,因此相等。
求解欧拉函数 $\varphi(n)$
$\varphi(n)$ 的值是 $\lbrace 1,2,3,\cdots,n\rbrace $ 中与 $n$ 互质的数的个数。
我们可以通过容斥原理来解决。
不妨对 $n$ 进行分解质因数:
\[n=p_1^{c_1}p_2^{c_2}p_3^{c_3}\cdots p_k^{c_k}\]其中,$p_i$ 为质数。
构造集合 $U=\lbrace1,2,3,\cdots,n\rbrace$,定义集合 $A_i=\lbrace x\in U \mid x \equiv 0 \pmod{p_i}\rbrace$,表示所有被 $p_i$ 整除的数的集合。
假定 $x$ 满足 $x$ 与 $n$ 互质,那么 $x$ 的质因子中一定不包含 $p_i(1\leq i\leq k)$。
因此 $\varphi(n)$ 即集合 $U$ 中不属于 $A_1,A_2,A_3,\cdots,A_n$ 中任意集合的元素的个数。
考虑到“补集的交等于并集的补”,有:
\[\begin{aligned} \varphi(n)&=\left\vert\overline{A_1}\bigcap\overline{A_2}\bigcap\overline{A_3}\bigcap\cdots\bigcap\overline{A_k}\right\vert\\ &=\vert U\vert-\vert A_1\bigcup A_2\bigcup A_3\bigcup\cdots\bigcup A_k\vert\\ &=n-\vert A_1\bigcup A_2\bigcup A_3\bigcup\cdots\bigcup A_k\vert \end{aligned}\]由容斥原理:
\[\begin{aligned} \vert A_1\bigcup A_2\bigcup A_3\bigcup\cdots\bigcup A_k\vert&=\left\vert\bigcup_{i=1}^kA_i\right\vert\\ &=\sum_{i=1}^k(-1)^{i-1}\sum_{1\leq a_1<a_2<\cdots<a_i\leq k}\left\vert\bigcap_{j=1}^iA_{a_j}\right\vert \end{aligned}\]对于 $[1,n]$ 内 $p$ 的倍数可以理解为以 $p$ 为周期,每周期一个,总个数为 $\left\lfloor\dfrac np\right\rfloor$,因此有:
\[\left\vert\bigcap_{j=1}^iA_{a_j}\right\vert=\left\lfloor\frac{n}{p_{a_1}p_{a_2}p_{a_3}\cdots p_{a_i}}\right\rfloor\]考虑到保证 $p_i$ 为 $n$ 的质因子,即 $n\bmod p_i=0$,则:
\[\left\vert\bigcap_{j=1}^iA_{a_j}\right\vert=\frac{n}{p_{a_1}p_{a_2}p_{a_3}\cdots p_{a_i}}\]那么,有:
\[\begin{aligned} \varphi(n)&=n-\left(\sum_{i=1}^k(-1)^{i-1}\sum_{1\leq a_1<a_2<a_3<\cdots<a_i\leq k}\frac{n}{p_{a_1}p_{a_2}p_{a_3}\cdots p_{a_i}}\right)\\ &=n-\sum_{1\leq i\leq k}\frac{n}{p_i}+\sum_{1\leq i<j\leq k}\frac{n}{p_ip_j}-\cdots+(-1)^{n-1}\frac{n}{p_1p_2p_3\cdots p_n}\\ &=n\left(1-\sum_{1\leq i\leq k}\frac{1}{p_i}+\sum_{1\leq i<j\leq k}\frac{1}{p_ip_j}-\cdots+(-1)^{n-1}\frac{1}{p_1p_2p_3\cdots p_n}\right)\\ &=n\left(1-\frac{1}{p_1}\right)\left(1-\frac{1}{p_2}\right)\left(1-\frac{1}{p_2}\right)\cdots\left(1-\frac{1}{p_k}\right)\\ &=n\prod_{i=1}^k\frac{p_i-1}{p_i} \end{aligned}\]例如:$735=3\times5\times7^2$。则 $\varphi(735)=735\times\dfrac23\times\dfrac45\times\dfrac67=336$。
广义容斥原理
设 $P_1,P_2,P_3,\cdots,P_n$ 为集合 $S$ 中所有可能的性质,令集合 $A_i$ 为 $S$ 中所有具有性质 $P_i$ 的元素的集合。
$\alpha(k)$ 与 $\beta(k)$ 的定义
记 $\alpha(k)$ 为“至少”具有 $k$ 个性质的元素个数(但元素满足多个性质时,会重复计数)。
\[\begin{aligned} &\alpha(0)=\vert S\vert\\ &\alpha(1)=\sum_{i=1}^n\vert A_i\vert\\ &\alpha(2)=\sum_{1\leq i<j\leq n}\vert A_i\bigcap A_j\vert\\ &\alpha(n)=\vert A_1\bigcap A_2\bigcap A_3\bigcap\cdots\bigcap A_n\vert\\ &\alpha(k)=\sum_{1\leq i_1<i_2<\cdots<i_k\leq n}\left\vert\bigcap_{i=i_1}^{i_k}A_i\right\vert \end{aligned}\]记 $\beta(k)$ 为恰好具有 $k$ 个性质的元素个数(不会重复计数)。
\[\begin{aligned} &\beta(0)=\left\vert\overline{A_1}\bigcap\overline{A_2}\bigcap\overline{A_3}\bigcap\cdots\bigcap\overline{A_n}\right\vert\\ &\beta(1)=\sum_{i=1}^n\left\vert A_i\bigcap\left(\bigcap_{1\leq j\leq n,j\ne i}\overline{A_j}\right)\right\vert\\ &\beta(2)=\sum_{1\leq i<j\leq n}\left\vert A_i\bigcap A_j\bigcap\left(\bigcap_{1\leq k\leq n,k\ne i,k\ne j}\overline{A_k}\right)\right\vert\\ &\beta(n)=\vert A_1\bigcap A_2\bigcap A_3\bigcap\cdots\bigcap A_n \vert\\ &\beta(k)=\sum_{1\leq i_1<i_2<\cdots<i_k\leq n}\left\vert\left(\bigcap_{j=1}^kA_{i_j}\right)\bigcap\left(\bigcap_{1\leq j\leq n,j\ne i_1,j\ne i_2,\cdots,j\ne i_k}\overline{A_j}\right)\right\vert \end{aligned}\]$\alpha(k)$ 与 $\beta(k)$ 的关系
\[\beta(k)=\alpha(k)-\binom{k+1}{k}\alpha(k+1)+\binom{k+2}{k}\alpha(k+2)-\cdots+(-1)^{n-k}\binom{n}{k}\alpha(n)\]证明
取一元素 $x$,拥有 $y$ 个性质。
若 $y<k$,则由 $\alpha(k),\beta(k)$ 的定义可知元素 $x$ 对等式左右两侧的数值没有影响。
若 $y=k$,则由 $\alpha(k),\beta(k)$ 的定义可知元素 $x$ 对等式左右两侧的数值的贡献均为 $1$。
若 $y>k$,则由 $\alpha(k),\beta(k)$ 的定义可知元素 $x$ 对等式左侧的贡献为 $0$,对等式右侧的贡献为:
$$ \begin{aligned} &\ \ \binom{y}{k}-\binom{k+1}{k}\binom{y}{k+1}+\binom{k+2}{k}\binom{y}{k+2}-\cdots+(-1)^{y-k}\binom{y}{k}\binom{y}{y}\\ &=\binom{y}{k}-\binom{y}{k}\binom{y-k}{1}+\binom{y}{k}\binom{y-k}{2}-\cdots+(-1)^{y-k}\binom{y}{k}\binom{y-k}{y-k}\\ &=\binom{y}{k}\left[\binom{y-k}{0}-\binom{y-k}{1}+\binom{y-k}{2}-\cdots+(-1)^{y-k}\binom{y-k}{y-k}\right]\\ &=0\\ \end{aligned} $$
上述变形过程中使用了公式:
$$ \binom{r}{k}\binom{n}{r}=\binom{n}{k}\binom{n-k}{r-k}\\ \sum_{i=0}^n(-1)^i\binom{n}{i}=[n=0] $$
详见二项式推论。
故对于任意 $x\in S$ 对于等式左右两侧的影响均相等,则等式左右两侧相等。
证毕。
不定方程非负整数解计数
已知 $x_1+x_2+x_3+\cdots+x_n=m$,求 $x_1,x_2,x_3,\cdots,x_n$ 的非负整数解组的个数。
对于这类问题,一个隐藏的条件即 $0\leq x_i\leq m$。
无限制
显然,问题等价于将 $m$ 个无区别的球放入 $n$ 个有区别的盒子,盒子可以为空。
由球盒问题,答案为:
\[\binom{m+n-1}{m}\]限制 $x_i\leq b_i$
因为 $x_i$ 为整数,所以 $x_i< b_i$ 的问题就是 $x_i\leq b_i-1$,本质上是一样的。
我们可以抽象出数学容斥模型:
- 全集 $U$:$x_1,x_2,x_3,\cdots,x_n$ 的所有取值可能,$\vert U\vert=$。
- 元素:变量 $x_i$.
- 元素性质:$x_i$ 的性质 $P_i$ 即 $x_i\leq b_i$。
令集合 $S_i$ 表示 $x_i$ 满足 $x_i\leq b_i$ 时的所有可能情况。
答案即所有 $x_i$ 均满足其性质 $x_i\leq b_i$ 时的可能情况,即:
\[\vert S_1\cap S_2\cap S_3\cap\cdots\cap S_n\vert=\vert U\vert-\left\vert\overline{S_1}\cup\overline{S_2}\cup\overline{S_3}\cup\cdots\cup\overline{S_n}\right\vert\]错排问题
又称错位排列问题,即对于 $\lbrace1,2,3,\cdots,n\rbrace$ 的排列 $P$,如果满足不存在 $P_i=i$,则称排列 $P$ 是一个错位排列。
令 $D_n$ 表示 $\lbrace1,2,3,\cdots,n\rbrace$ 的错位排列的个数,定义 $D_1=0,D_2=1$,有:
\[D_n=(n-1)(D_{n-1}+D_{n-2})\]证明
假设已经得到了一个长度为 $n-1$ 的 $\lbrace1,2,3,\cdots,n-1\rbrace$ 的排列 $P$,分类讨论:
- $P_1\sim P_{n-1}$ 中不存在 $P_i=i$:选择一个与 $P_n=n$ 交换即可得到长度为 $n$ 的错位排列,对答案的贡献为 $(n-1)D_{n-1}$。
-
$P_1\sim P_{n-1}$ 中存在一个 $P_i=i$:将其与 $P_n=n$ 交换即可得到长度为 $n$ 的错位排列。
那么这种情况对答案的贡献就是 $(n-1)D_{n-2}$,因为除 $P_i=i$ 外的 $n-2$ 个元素是一个错位排列。
-
$P_1\sim P_{n-1}$ 中含有至少 $2$ 个 $P_i=i$:这种情况不可能使 $1\sim P_n$ 为错位排列,贡献为 $0$。
由加法原理,合并贡献得到 $D_n=(n-1)(D_{n-1}+D_{n-2})$。
变形上式,得到:
\[\begin{aligned} D_n&=n\cdot D_{n-1}-D_{n-1}+(n-1)D_{n-2}\\ D_n-n\cdot D_{n-1}&=(-1)^1[D_{n-1}-(n-1)D_{n-2}]\\ D_n-n\cdot D_{n-1}&=(-1)^2[D_{n-2}-(n-2)D_{n-3}]\\ D_n-n\cdot D_{n-1}&=(-1)^3[D_{n-3}-(n-3)D_{n-4}]\\ &\cdots\\ D_n-n\cdot D_{n-1}&=(-1)^{n-1}[D_1-D_0]\\ D_n-n\cdot D_{n-1}&=(-1)^{n-1}\\ D_n&=n\cdot D_{n-1}+(-1)^n \end{aligned}\]$D_0$ 没有意义。
但实际上还有一个看起来非常天才的表示方法:
\[D_n=\begin{cases} \left\lfloor\dfrac{n!}e\right\rfloor&n\bmod 2=1\\ \left\lceil\dfrac{n!}e\right\rceil&n\bmod2=0 \end{cases}\]但是这在 OI 中基本没用,因为模意义下不能取整。(但是这告诉我们,错位排列的密度大约为 $\dfrac1e$)。
容斥原理一般化
对于两个对于集合的函数 $f(S),g(S)$:
-
若 $g(S)=\sum\limits_{T\subseteq S}f(T)$,则有:
\(f(S)=\sum_{T\subseteq S}(-1)^{\vert S\vert-\vert T\vert}g(T)\) 二项式反演即容斥原理的特殊形式。
-
若 $g(S)=\sum\limits_{T\supseteq S}f(T)$,则有: \(f(S)=\sum_{T\supseteq S}(-1)^{\vert T\vert-\vert S\vert}g(T)\)
Min-max 容斥
对于满足全序关系且可加减的序列 $\langle x_1,x_2,\cdots,x_n\rangle$,设 $S=\lbrace1,2,3,\cdots,n\rbrace$,有:
\[\begin{aligned} \max_{i\in S}x_i&=\sum_{T\subseteq S}(-1)^{\vert T\vert-1}\min_{i\in T}x_i\\ \min_{i\in S}x_i&=\sum_{T\subseteq S}(-1)^{\vert T\vert-1}\max_{i\in T}x_i \end{aligned}\]这对于期望也是存在的,因此常常在求解期望问题中用到。
即:
\[\begin{aligned} E\left(\max_{i\in S}x_i\right)&=\sum_{T\subseteq S}(-1)^{\vert T\vert-1}E\left(\min_{i\in T}x_i\right)\\ E\left(\min_{i\in S}x_i\right)&=\sum_{T\subseteq S}(-1)^{\vert T\vert-1}E\left(\max_{i\in T}x_i\right)\\ \end{aligned}\]kth Min-Max 容斥
记 $\operatorname{kthmax}$ 表示第 $k$ 大的元素,$\operatorname{kthmin}$ 同理。
则有:
\[\begin{aligned} \operatorname*{kthmax}_{i\in S}x_i&=\sum_{T\subseteq S}(-1)^{\vert T\vert-k}\dbinom{\vert T\vert-1}{k-1}\min_{i\in T}x_i\\ \operatorname*{kthmin}_{i\in S}x_i&=\sum_{T\subseteq S}(-1)^{\vert T\vert-k}\dbinom{\vert T\vert-1}{k-1}\max_{i\in T}x_i\\ E\left(\operatorname*{kthmax}_{i\in S}x_i\right)&=\sum_{T\subseteq S}(-1)^{\vert T\vert-k}\dbinom{\vert T\vert-1}{k-1}E\left(\min_{i\in T}x_i\right)\\ E\left(\operatorname*{kthmin}_{i\in S}x_i\right)&=\sum_{T\subseteq S}(-1)^{\vert T\vert-k}\dbinom{\vert T\vert-1}{k-1}E\left(\max_{i\in T}x_i\right)\\ \end{aligned}\]kth Min-max 容斥常常配合期望、DP 出现。对于这种情况下的 DP 的转移方程,可以参考组合数递推公式。
gcd-lcm 容斥
对于集合 $T$,有:
\[\operatorname*{lcm}_{i\in T}i=\prod_{S\subseteq T}\left(\gcd_{i\in S}i\right)^{(-1)^{\vert S\vert-1}}\]将每一个质数分开考虑即可得出上述结论。对于质数 $p$:
\[\begin{aligned} \operatorname{lcm}\left(p^a,p^b\right)&=p^{\max(a,b)}\\ \gcd\left(p^a,p^b\right)&=p^{\min(a,b)} \end{aligned}\]套用 Min-max 容斥即可。
P3598 Koishi Loves Number Theory
对于常数 $x$,定义 $f(n)=\sum\limits_{i=0}^nx^i$。
给定 $n$ 和 $a_1,a_2,\cdots,a_n$,求 $\operatorname{lcm}(f(a_1),f(a_2),\cdots,f(a_n))$。
参见此处。
鸽巢原理
引入
$6$ 只鸽子在 $5$ 个鸽巢中,请问鸽子最多的鸽巢里最少有几只鸽子?
很显然,是 $2$ 只,因为可以考虑一种最坏的情况——平均分配。那么分配了 $5$ 只鸽子后,多出来一只无论分配到哪一个鸽巢,都会使该鸽巢有 $2$ 只鸽子。
定义
鸽巢原理,亦称抽屉原理。
它常被用于证明存在性证明和求最坏情况下的解。
推广
将 $n$ 个物品划分为 $k$ 组,则至少存在一个分组,含有至少 $\left\lceil\dfrac{n}{k}\right\rceil$ 个物品。
证明只需要考虑反证即可。假设不存在一个分组,含有至少 $\left\lceil\dfrac{n}{k}\right\rceil$ 个物品,即所有分组至多有 $\left\lceil\dfrac{n}{k}\right\rceil-1$ 个物品。
则总共最多物品数为 $k\left(\left\lceil\dfrac nk\right\rceil-1\right)=k\left\lceil\dfrac nk\right\rceil-k$。因为 $\left\lceil\dfrac nk\right\rceil<\dfrac nk+1$,所以 $k\left\lceil\dfrac nk\right\rceil-k<n$,即总物品数小于 $n$。然而总物品数为 $n$,因此假设不成立。