有向图没有点双连通分量
有向图请见强连通分量。
点双连通分量
点双连通
若一个无向连通图删去任意一个点之后仍然连通,则该图点双连通。
点双连通分量
在满足边双连通的前提下尽可能大的子图。
Tarjan 求点双连通分量
前置知识:Tarjan 求割点
Tarjan 求点双连通分量
三条性质
-
两个点双连通分量存在至多一个公共点。
证明
假设两个点双连通分量可以存在至少两个公共点。
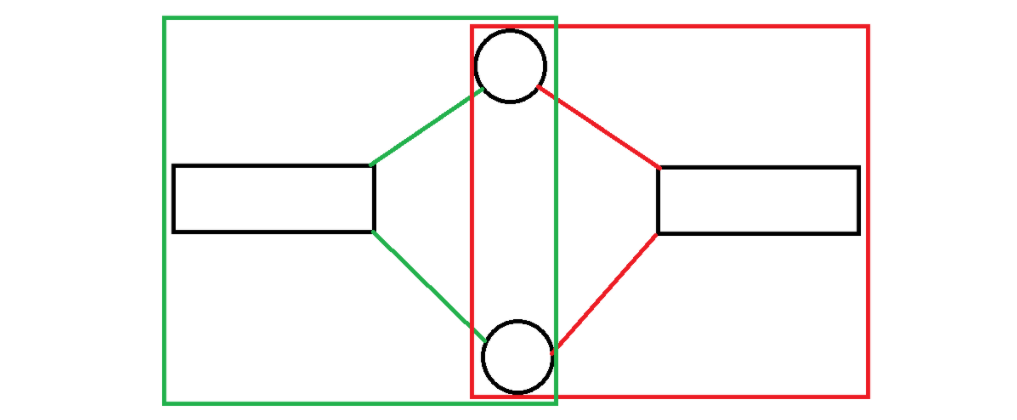
如图中绿色点双连通分量和红色点双连通分量,显然将二者合并之后仍然满足点双连通分量的定义,因此二者都不是点双连通分量(不满足“极大”)。
与假设矛盾,故原命题成立。
-
两个点双连通分量的公共点如果存在则一定是割点。
证明
假设两个点双连通分量存在的公共点不为割点。
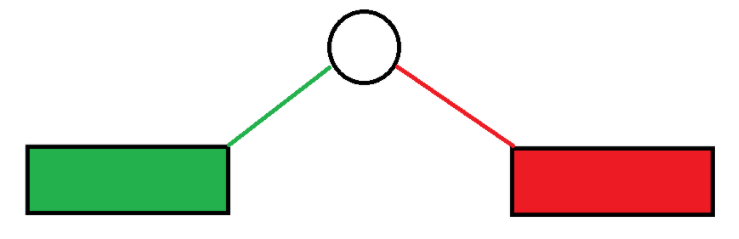
则如图所示,由割点的性质,断开并不会导致不连通,因此绿色部分和红色部分也可以合并,因此绿色部分和红色部分都不为强连通分量。
与假设矛盾,故原命题成立。
-
点双连通分量内 $dfn$ 最小的节点一定是割点或 DFS 生成树的根节点。
证明
令某点双连通分量内 $dfn$ 最小的节点为 $x$。
-
当 $x$ 为根节点时:
显然成立。因为在 DFS 生成树中,深度最小的节点 $dfn$ 最小,最小时可以显然为根节点。
-
当 $x$ 不为根节点时:
假设节点 $x$ 不为割点。
那么将该点双连通分量与 $x$ 的父节点合并到一起,显然可以成为一个点双连通分量,则 $x$ 不是 $dfn$ 最小的节点。
与假设矛盾,故此种情况下原命题成立。
证毕。
-
分类讨论
分类讨论:
- 当节点 $x$ 为割点时,则点 $x$ 一定是某个点双连通分量在 DFS 生成树上的根节点。
- 当节点 $x$ 为 DFS 生成树的根节点时:
- 子树不存在,则节点 $x$ 是一个孤立点,视为一个点双连通分量(的根节点)。
- 存在一棵子树,则节点 $x$ 是点双连通分量的根节点。
- 存在至少两棵子树,则节点 $x$ 是割点(可以参考割点的判定),即某个点双连通分量在 DFS 生成树上的根节点。
总结一下就可以发现,点双连通分量一定在割点或根节点的子树中。
用一个栈维护节点,那么在找到割点或根节点时,将其子树内的点归到一个新的点双即可。
如何确保子树内的点一定属于这个点双连通分量
由 DFS 生成树和递归,递归至当前的 $x$ 时,$x$ 子树内可能会存在其他点双连通分量,但是这些点双连通分量已经出栈(暂不考虑割点和根节点),因此在求解 $x$ 时并不会影响到。
对于割点 $y$,如果在求解 $x$ 时在栈内,说明 $x,y$ 所在点双连通分量的公共节点是 $y$,$y$ 应当被出栈记录。
对于根节点,显然只会是栈底,且只有自己能够访问到,不影响答案的正确性。
注意这个点可能还是与其它点双的公共点,所以不能将其出栈,只应当出栈到其子节点。
例题 AC 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=5e5,M=2e6;
struct graph{
struct edge{
int v,r;
}a[2*M+1];
int h[N+1];
void create(int u,int v){
static int top=1;
a[++top]={v,h[u]};
h[u]=top;
}
}g;
int dfn[N+1];
int ansSize;
vector<int>ans[N+1];
void Tarjan(int x,int fx){
static int s[N+1];
static int top,cnt,low[N+1];
dfn[x]=low[x]=++cnt;//不要混用top和cnt!!
s[++top]=x;
int son=0;
for(int i=g.h[x];i;i=g.a[i].r){
int &v=g.a[i].v;
if(v==fx)continue;
if(!dfn[v]){
son++;
Tarjan(v,x);
low[x]=min(low[x],low[v]);
/*
是割点或根节点。
割点很好理解,见"无向图 Tarjan 割点详解"。
至于根节点,dfn[root]本来就是最小值,一定成立。
*/
if(low[v]>=dfn[x]){
ansSize++;
ans[ansSize].resize(0);
while(s[top]!=v){
ans[ansSize].push_back(s[top--]);
}
ans[ansSize].push_back(s[top--]);
ans[ansSize].push_back(x);
}
}else low[x]=min(low[x],dfn[v]);
}//没有父节点和子节点,孤立点
if(!fx&&!son)ans[++ansSize].push_back(x);
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
int n,m;
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++){
int u,v;
scanf("%d %d",&u,&v);
if(u==v)continue;//剔除自环!!!
g.create(u,v);
g.create(v,u);
}
for(int i=1;i<=n;i++){
if(!dfn[i])Tarjan(i,0);
}
printf("%d\n",ansSize);
for(int i=1;i<=ansSize;i++){
printf("%d",ans[i].size());
for(int &j:ans[i])printf(" %d",j);
putchar(10);
}
/*fclose(stdin);
fclose(stdout);*/
return 0;
}