点分治
基本原理
点分治,即将树以节点为分界点划分为若干个部分,从而将一个大规模问题转化为了若干个相同的小规模问题,从而解答。
点分治常常用于处理树上路径信息。
考虑一棵树,根节点为 $x$,子节点分别为 $v_1,v_2,\cdots,v_s$。
那么这棵树内,路径可以被分为两种:
- 经过 $x$,从子树 $v_i$ 出发,到达子树 $v_j$ 内部的。(也可以一端在在 $x$ 上)
- 完全在子树 $v_i$ 内部的。
那么,完全在子树 $v_i$ 内部的问题和树 $x$ 内部的问题是一样的规模更小的问题。因此我们只需要想办法处理经过 $x$ 的路径信息,就可以递归解决。
而为了取到最优复杂度,我们每次会选取树的重心作为一个连通块的根节点处理,处理完后删除这个节点,并递归处理其子节点即可。
重心,保证了其余子树最大大小不超过树的大小的一半,因此每次减半,至多会递归 $\mathcal O(\log n)$ 层。
点分治复杂度与重心
如果你的重心找的是错的,那么你点分治的答案不会有错,但是复杂度会假。
因此如果你的点分治跑的很慢,可以检查你的重心。
实现模板
找重心就先 DFS 一遍(任意节点 $x$ 为根)求每个节点的子树大小,之后就可以用 $\displaystyle\textit{size}x-\sum{i=1}^y\textit{size}_{v_i}$ 表示剩余部分的大小。最终满足以下条件即为重心:
\[\max\left(\textit{size}_x-\sum_{i=1}^y\textit{size}_{v_i},\textit{size}_{v_1},\textit{size}_{v_2},\cdots,\textit{size}_{v_y}\right)\leq\dfrac{\textit{size}_x}{2}\]
同时要注意点分治常数较大,因此尽量只点分治一次,集中处理所有询问。
参考代码
```cpp
//#include<bits/stdc++.h>
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
constexpr const int N=1e4;
int n;
vector<pair<int,int>>g[N+1];
bool del[N+1];
void dfs1(int x,int fx,int size[]){
size[x]=1;
for(auto [v,w]:g[x]){
if(v==fx||del[v]){
continue;
}
dfs1(v,x,size);
size[x]+=size[v];
}
}
int dfs2(int x,int fx,int n,int size[]){
int Max=n-size[x];
for(auto [v,w]:g[x]){
if(v==fx||del[v]){
continue;
}
Max=max(Max,size[v]);
}
if(Max<=(n>>1)){
return x;
}else{
for(auto [v,w]:g[x]){
if(v==fx||del[v]){
continue;
}
int p=dfs2(v,x,n,size);
if(p!=-1){
return p;
}
}
}
return -1;
}
int root(int x){
static int size[N+1];
dfs1(x,0,size);
return dfs2(x,0,size[x],size);
}
void dfs3(int x,int fx,/*...*/){
//...
for(auto [v,w]:g[x]){
if(v==fx||del[v]){
continue;
}
dfs3(v,x,/*...*/);
}
}
void solve(int x){
//...
//w:边的信息
for(auto [v,w]:g[x]){
if(del[v]){
continue;
}
//pl:记录子树 v 内的信息
vectorpl;
dfs3(v,x,w,pl);
//...处理 pl
for(int i:pl){
//...将信息更新到前面的子树的信息上
}
}
del[x]=true;
for(auto [v,w]:g[x]){
if(del[v]){
continue;
}
solve(root(v));
}
}
//...
solve(root(/*任意节点*/));
//...
```
</details>
## 例题
### [Luogu P3806 点分治](https://www.luogu.com.cn/problem/P3806)
> 给定一棵 $n$ 个点的数,询问树上距离为 $k_1,k_2,\cdots,k_m$ 的点对是否存在。
>
> $1\leq n\leq10^4,1\leq m\leq100,1\leq k_i\leq10^7$。
设根节点为 $x$,$x$ 的子节点分别为 $v_1,v_2,\cdots,v_{y}$。
假设现在在处理 $k_j$。
那么我们就分别 DFS 子树 $v_1,v_2,\cdots,v_y$。处理到子树 $v_i$ 时,我们想要让子树 $v_i$ 中的点和子树 $v_1,v_2,\cdots,v_{i-1}$ 中的点组成距离为 $k_j$ 的点对。
无边权,则可以在 DFS 过程中处理节点 $p$ 的深度 $\textit{depth}_p$($\textit{depth}_x=0$),节点 $p,q$ 的距离为 $k_j$ 即:
$$
\textit{depth}_p+\textit{depth}_q=k_j
$$
考虑 $q$ 在子树 $v_i$ 内,则只需要快速找到一个 $p$ 在前面的子树内,且 $\textit{depth}_p=k_j-\textit{depth}_q$。
那么我们考虑维护一个标记 $\textit{flag}_l$ 表示 $\textit{depth}_p=l$ 是否在子树 $v_1,v_2,\cdots,v_{i-1}$ 内出现过。
子树 $v_i$ DFS 结束之后就是将每一个点的信息在 $\textit{flag}$ 上查询,更新答案。$v_i$ 子树查询结束后,就将子树 $v_i$ 的信息合并到前面的子树信息上,即 $\textit{flag}$ 上。
这样处理,遍历一个连通块的复杂度为 $\mathcal O(\textit{size}_x)$ 。考虑一层之内,总复杂度为 $\mathcal O(m\sum\textit{size}_x)=\mathcal O(nm)$,则总复杂度为 $\mathcal O(nm\log n)$。
***
点分治还需要考虑清空,一般时间戳优化即可。
参考代码
```cpp
//#include<bits/stdc++.h>
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
constexpr const int N=1e4,M=100,K=1e7;
int n,m,k[M+1];
vector<pair<int,int>>g[N+1];
bool del[N+1],ans[M+1];
void dfs1(int x,int fx,int size[]){
size[x]=1;
for(auto [v,w]:g[x]){
if(v==fx||del[v]){
continue;
}
dfs1(v,x,size);
size[x]+=size[v];
}
}
int dfs2(int x,int fx,int n,int size[]){
int Max=n-size[x];
for(auto [v,w]:g[x]){
if(v==fx||del[v]){
continue;
}
Max=max(Max,size[v]);
}
if(Max<=(n>>1)){
return x;
}else{
for(auto [v,w]:g[x]){
if(v==fx||del[v]){
continue;
}
int p=dfs2(v,x,n,size);
if(p!=-1){
return p;
}
}
}
return -1;
}
int root(int x){
static int size[N+1];
dfs1(x,0,size);
return dfs2(x,0,size[x],size);
}
void dfs3(int x,int fx,int d,vector&dis){
dis.push_back(d);
for(auto [v,w]:g[x]){
if(v==fx||del[v]){
continue;
}
dfs3(v,x,d+w,dis);
}
}
void solve(int x){
static int tag[K+1];
static bool flag[K+1];
tag[0]++;
flag[0]=true;
for(auto [v,w]:g[x]){
if(del[v]){
continue;
}
vectorpl;
dfs3(v,x,w,pl);
for(int i=1;i<=m;i++){
if(ans[i]){
continue;
}
for(int j:pl){
if(0<=k[i]-j&&k[i]-j<=K){
if(tag[k[i]-j]!=tag[0]){
tag[k[i]-j]=tag[0];
flag[k[i]-j]=false;
}
if(flag[k[i]-j]){
ans[i]=true;
break;
}
}
}
}
for(int i:pl){
if(0<=i&&i<=K){
flag[i]=true;
tag[i]=tag[0];
}
}
}
del[x]=true;
for(auto [v,w]:g[x]){
if(del[v]){
continue;
}
solve(root(v));
}
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<n;i++){
int u,v,w;
cin>>u>>v>>w;
g[u].push_back({v,w});
g[v].push_back({u,w});
}
for(int i=1;i<=m;i++){
cin>>k[i];
}
solve(root(1));
for(int i=1;i<=m;i++){
cout<<(ans[i]?"AYE\n":"NAY\n");
}
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
### [Luogu P4178 Tree](https://www.luogu.com.cn/problem/P4178)
> 给定一棵 $n$ 个节点的树,每条边有边权 $w$,求出树上两点距离小于等于 $k$ 的点对数量。
>
> $1\leq n\leq4\times10^4,0\leq w\leq10^3,0\leq k\leq2\times10^4$.
树上路径信息,考虑点分治,处理经过根节点 $x$ 的路径。
当前子树中有一个点到 $i$ 距离为 $\textit{dis}_i$,那么我们想在之前的子树中找到 $j$ 的数量,满足:
$$
\begin{aligned}
\textit{dis}_i+\textit{dis}_j&\leq k\\
\textit{dis}_j&\leq k-\textit{dis}_i
\end{aligned}
$$
显然可以用树状数组/线段树维护。
总时间复杂度 $\mathcal O\left(n\log^2n\right)$。
参考代码
```cpp
//#include<bits/stdc++.h>
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
constexpr const int N=4e4,K=2e4+1;
int n,k,ans;
vector<pair<int,int>>g[N+1];
bool del[N+1];
void dfs1(int x,int fx,int size[]){
size[x]=1;
for(auto [v,w]:g[x]){
if(v==fx||del[v]){
continue;
}
dfs1(v,x,size);
size[x]+=size[v];
}
}
int dfs2(int x,int fx,int n,int size[]){
int Max=n-size[x];
for(auto [v,w]:g[x]){
if(v==fx||del[v]){
continue;
}
Max=max(Max,size[v]);
}
if(Max<=(n>>1)){
return x;
}else{
for(auto [v,w]:g[x]){
if(v==fx||del[v]){
continue;
}
int p=dfs2(v,x,n,size);
if(p!=-1){
return p;
}
}
}
return -1;
}
int root(int x){
static int size[N+1];
dfs1(x,0,size);
return dfs2(x,0,size[x],size);
}
void dfs3(int x,int fx,int d,vector&dis){
dis.push_back(d);
for(auto [v,w]:g[x]){
if(v==fx||del[v]){
continue;
}
dfs3(v,x,d+w,dis);
}
}
struct bit{
int t[K+1],tag[K+1],Tag;
int lowbit(int x){
return x&-x;
}
void add(int x,int k){
x++;
if(x<1||K<x){
return;
}
while(x<=K){
if(tag[x]!=Tag){
tag[x]=Tag;
t[x]=0;
}
t[x]+=k;
x+=lowbit(x);
}
}
int query(int x){
int ans=0;
x++;
if(x<1||K<x){
return 0;
}
while(x){
if(tag[x]!=Tag){
tag[x]=Tag;
t[x]=0;
}
ans+=t[x];
x-=lowbit(x);
}
return ans;
}
void clear(){
Tag++;
}
}t;
void solve(int x){
t.clear();
t.add(0,1);
for(auto [v,w]:g[x]){
if(del[v]){
continue;
}
vectorpl;
dfs3(v,x,w,pl);
for(int i:pl){
ans+=t.query(k-i);
}
for(int i:pl){
t.add(i,1);
}
}
del[x]=true;
for(auto [v,w]:g[x]){
if(del[v]){
continue;
}
solve(root(v));
}
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n;
for(int i=1;i<n;i++){
int u,v,w;
cin>>u>>v>>w;
g[u].push_back({v,w});
g[v].push_back({u,w});
}
cin>>k;
solve(root(1));
cout<<ans<<'\n';
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
### [Luogu P3714 [BJOI2017] 树的难题](https://www.luogu.com.cn/problem/P3714)
> 给定 $n$ 个点的无根树,每条边都有颜色。颜色共 $m$ 种,颜色 $i$ 的权值为 $a_i$。
>
> 定义路径权值为路径的颜色序列上每个同颜色段的颜色权值之和。
>
> 求经过边数在 $[L,R]$ 内的简单路径中,路径权值的最大值。
>
> $1\leq n,m\leq2\times10^5$,$\vert c_i\vert\leq10^4$。
树上路径信息,考虑点分治。
那么对于经过根节点 $x$ 的路径 $i\sim j$,设 $i$ 在 $x$ 子节点 $v_i$ 子树内,$j$ 在 $x$ 子节点 $v_j$ 子树内。
显然路径权值与 $(x,v_i),(x,v_j)$ 的颜色相关,它们颜色相同/不同时贡献不一样。因此考虑将颜色相同的放在一起,即将每个点的边按照颜色从小到大排序。
之后考虑 $v_i$ 子树内的节点 $i$ 到之前子树 $v_j$ 内的节点 $j$ 的路径权值。记 $c_{v_i}$ 表示边 $(x,v_i)$ 的颜色,$w_i$ 表示 $x\sim i$ 的路径权值(这很好用 DFS 直接求出),则 $i\sim j$ 的路径权值为:
$$
\begin{cases}
w_i+w_j&c_{v_i}\neq c_{v_j}\\
w_i+w_j-a_{c_{v_i}}&c_{v_i}=c_{v_j}
\end{cases}
$$
同时,$j$ 需要满足:
$$
\textit{depth}_i+\textit{depth}_j\in[L,R]
$$
即:
$$
\textit{depth}_j\in\left[L-\textit{depth}_i,R-\textit{depth}_j\right]
$$
先不考虑 $c_{v_i},c_{v_j}$ 的影响,求 $i$ 得最大路径权值即求满足 $\textit{depth}_j\in\left[L-\textit{depth}_i,R-\textit{depth}_j\right]$ 的 $w_j$ 的最大值。显然可以线段树维护区间 $\max$。
考虑到 $c_{v_i},c_{v_j}$ 的影响后,就可以考虑把之前所有颜色建一棵线段树 $t_1$ 维护,当前颜色建一棵线段树 $t_2$ 维护;这样就可以分开计算。颜色变更时,就将 $t_2$ 合并到 $t_1$ 上,重建 $t_2$ 即可。
时间复杂度 $\mathcal O\left(n\log^2n\right)$。
注意维护线段树区间查询的时候,要特判 $r<1$;否则你的查询会炸。
参考代码
```cpp
//#include<bits/stdc++.h>
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
constexpr const int N=2e5,M=N;
constexpr const ll inf=0x3f3f3f3f3f3f3f3f;
int n,m,L,R,a[M+1];
bool del[N+1];
vector<pair<int,int>>g[N+1];
void dfs1(int x,int fx,int size[]){
size[x]=1;
for(auto [v,c]:g[x]){
if(v==fx||del[v]){
continue;
}
dfs1(v,x,size);
size[x]+=size[v];
}
}
int dfs2(int x,int fx,int n,int size[]){
int Max=n-size[x];
for(auto [v,c]:g[x]){
if(v==fx||del[v]){
continue;
}
Max=max(Max,size[v]);
}
if(Max<=(n>>1)){
return x;
}else{
for(auto [v,c]:g[x]){
if(v==fx||del[v]){
continue;
}
int p=dfs2(v,x,n,size);
if(p!=-1){
return p;
}
}
}
return -1;
}
int root(int x){
static int size[N+1];
dfs1(x,0,size);
return dfs2(x,0,size[x],size);
}
void dfs3(int x,int fx,int w0,int depth,int c0,vector<pair<int,int>>&info){
if(depth>R){
return;
}
info.push_back({w0,depth});
for(auto [v,c]:g[x]){
if(v==fx||del[v]){
continue;
}
dfs3(v,x,w0+(c!=c0)*a[c],depth+1,c,info);
}
}
namespace segTree{
int size;
struct node{
int l,r;
ll max;
int lChild,rChild;
}t[N*40+1];
void clear(){
size=0;
}
struct segTree{
int root;
int create(node x){
t[++size]=x;
return size;
}
void up(int p){
t[p].max=max(t[t[p].lChild].max,t[t[p].rChild].max);
}
void build(int l,int r){
root=create({l,r,-inf});
}
void down(int p){
int mid=t[p].l+t[p].r>>1;
if(!t[p].lChild){
t[p].lChild=create({t[p].l,mid,-inf});
}
if(!t[p].rChild){
t[p].rChild=create({mid+1,t[p].r,-inf});
}
}
void update(int p,int x,ll k){
if(t[p].l==t[p].r){
t[p].max=max(t[p].max,k);
return;
}
down(p);
if(x<=t[t[p].lChild].r){
update(t[p].lChild,x,k);
}else{
update(t[p].rChild,x,k);
}
up(p);
}
void update(int x,int k){
if(x<1||n<x){
return;
}
update(root,x,k);
}
ll query(int p,int l,int r){
if(l<=t[p].l&&t[p].r<=r){
return t[p].max;
}
down(p);
ll ans=-inf;
if(l<=t[t[p].lChild].r){
ans=query(t[p].lChild,l,r);
}
if(t[t[p].rChild].l<=r){
ans=max(ans,query(t[p].rChild,l,r));
}
return ans;
}
ll query(int l,int r){
if(r<1){
return -inf;
}
return query(root,l,r);
}
int merge(int x,int y){
if(!x||!y){
return x|y;
}
if(t[x].l==t[x].r){
t[x].max=max(t[x].max,t[y].max);
return x;
}
down(x);
t[x].lChild=merge(t[x].lChild,t[y].lChild);
t[x].rChild=merge(t[x].rChild,t[y].rChild);
up(x);
return x;
}
void merge(segTree &x){
root=merge(root,x.root);
}
}t1,t2;
}
using segTree::t1;
using segTree::t2;
ll ans=-inf;
void solve(int x,int tab=0){
segTree::clear();
t1.build(1,n);
t2.build(1,n);
int lastC=0;
for(auto [v,c]:g[x]){
if(del[v]){
continue;
}
if(c!=lastC){
lastC=c;
t1.merge(t2);
t2.build(1,n);
}
vector<pair<int,int>>info;
dfs3(v,x,a[c],1,c,info);
for(auto [w,depth]:info){
ans=max({ans,t1.query(L-depth,R-depth)+w,t2.query(L-depth,R-depth)-a[c]+w});
}
for(auto [w,depth]:info){
t2.update(depth,w);
if(L<=depth&&depth<=R){
ans=max(ans,1ll*w);
}
}
}
del[x]=true;
for(auto [v,c]:g[x]){
if(del[v]){
continue;
}
solve(root(v));
}
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m>>L>>R;
for(int i=1;i<=m;i++){
cin>>a[i];
}
for(int i=1;i<n;i++){
int u,v,c;
cin>>u>>v>>c;
g[u].push_back({v,c});
g[v].push_back({u,c});
}
for(int i=1;i<=n;i++){
sort(g[i].begin(),g[i].end(),[](pair<int,int>a,pair<int,int>b){
return a.second<b.second;
});
}
solve(root(1));
cout<<ans<<'\n';
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
# 边分治
## 基本原理
对于树上的一条边 $(u,v)$,将其断开后原树会变为**两棵**子树 $u,v$。考虑两棵子树的问题是一样的,可以递归处理。
那么只需要讨论经过 $(u,v)$ 的信息即可。
让左右子树尽可能大小接近,才能取到 $\mathcal O(\log n)$ 的最优递归层数。
### 三度化
但是容易发现,如果原树是一个菊花图,那么就会变成 $\mathcal O\left(n^2\right)$。本质上这是因为我们找不到一条边,能够将树分为两个大小尽可能接近的部分(子树大小接近)。
这个问题可以通过三度化解决,即建立一些**虚点**,使得树上每个点的度数都小于等于 $3$。
三度化主要有两种方法,以下图为例:
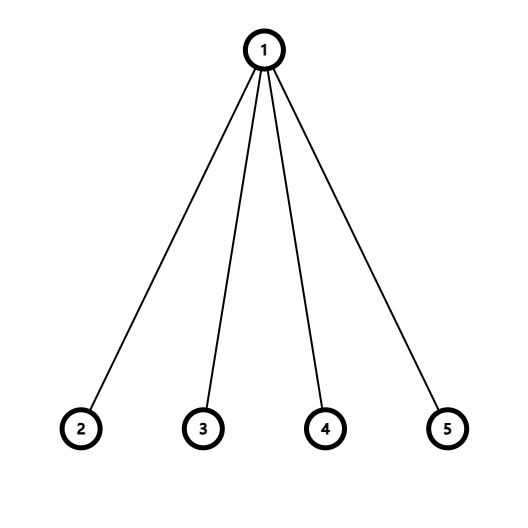
#### 链式
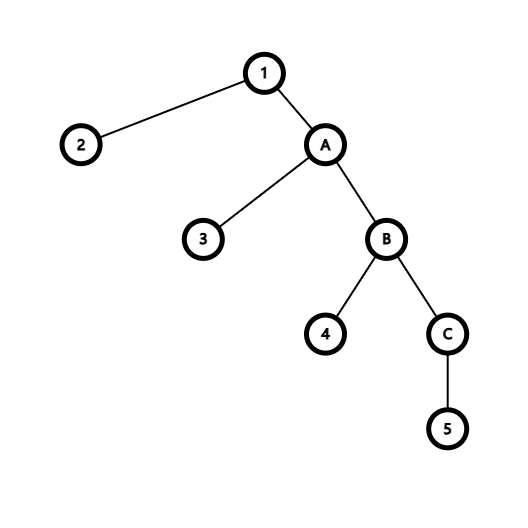
新建了节点 $\text{A,B,C,C}$,就使得每一个节点都是三度化的。
把子节点挂在一个虚点链上。
#### 线段树式
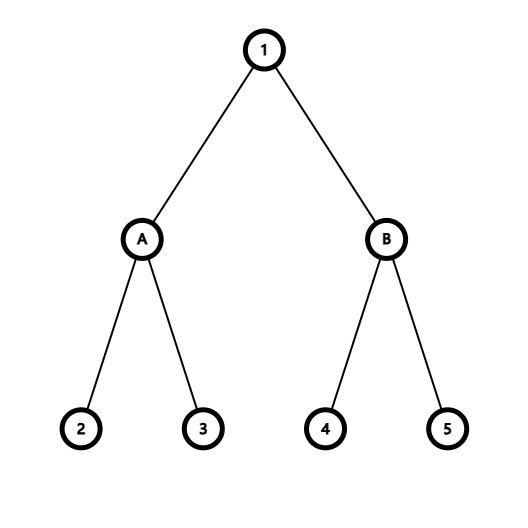
新建了节点 $\text{A,B}$,就使得每一个节点都是三度化的。
即类似于一棵线段树,原本的子节点为叶节点,原本父节点为根节点,其余均为虚点。
***
显然两种方法最终增加的节点数量均为 $\mathcal O(n)$。
每次将原树分为大小相近的 $2$ 部分,若单次处理复杂度 $\mathcal O(n)$。
## 合并果子点分治
考虑边分治要写三度化,可能不好写,因此我们还是想写点分治。如果说合并子树 $i,j$ 的信息,复杂度为 $\mathcal O(\textit{size}_i+\textit{size}_j)$,那么若按照子树大小从小到大合并,整个点分治的复杂度仍然为 $\mathcal O(n\log n)$。
因此边分治很多时候可以被此种方法代替。
#