笛卡尔树
定义
笛卡尔树是一种二叉树,每一个节点有两个权值 $a,b$,要求所有节点的 $a$ 满足 BST(二叉查找树)的性质,$b$ 满足堆[^1]的性质。若 $a,b$ 确定,则笛卡尔树是确定的。
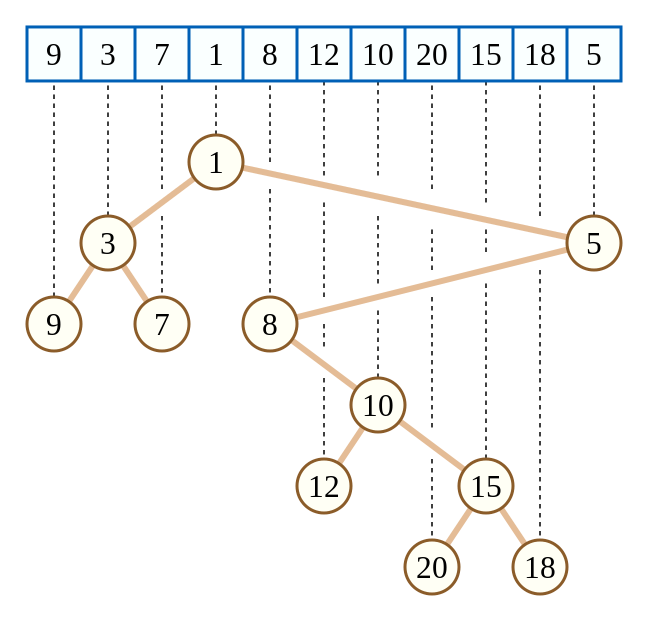
如图,取 $a=\langle1,2,3,4,5,6,7,8,9,10,11\rangle,b=\langle9,3,7,1,8,12,10,20,15,18,5\rangle$,即可构建上图。下标满足 BST 性质,值满足堆的性质。
同时,Treap 实际上就是一种笛卡尔树。
构建
笛卡尔树可以做到 $\mathcal O(n)$ 构建。
考虑按照满足 BST 性质的 $a$ 升序插入节点 $x$,那么节点 $x$ 要么是根节点,要么是最右端的节点。
考虑维护一条「右链」,即只包含根节点和右子节点的链。
插入节点 $x$ 时,找右链上的节点 $y$ 使得 $b_y\leq b_x$ 且 $b_y$ 最大($y$ 最深),则 $x$ 为 $y$ 的右子节点,$y$ 原来的右子节点 $v$ 现在为 $x$ 的左子节点。
特别地,若不存在 $b_y\leq b_x$,则 $x$ 为根节点。
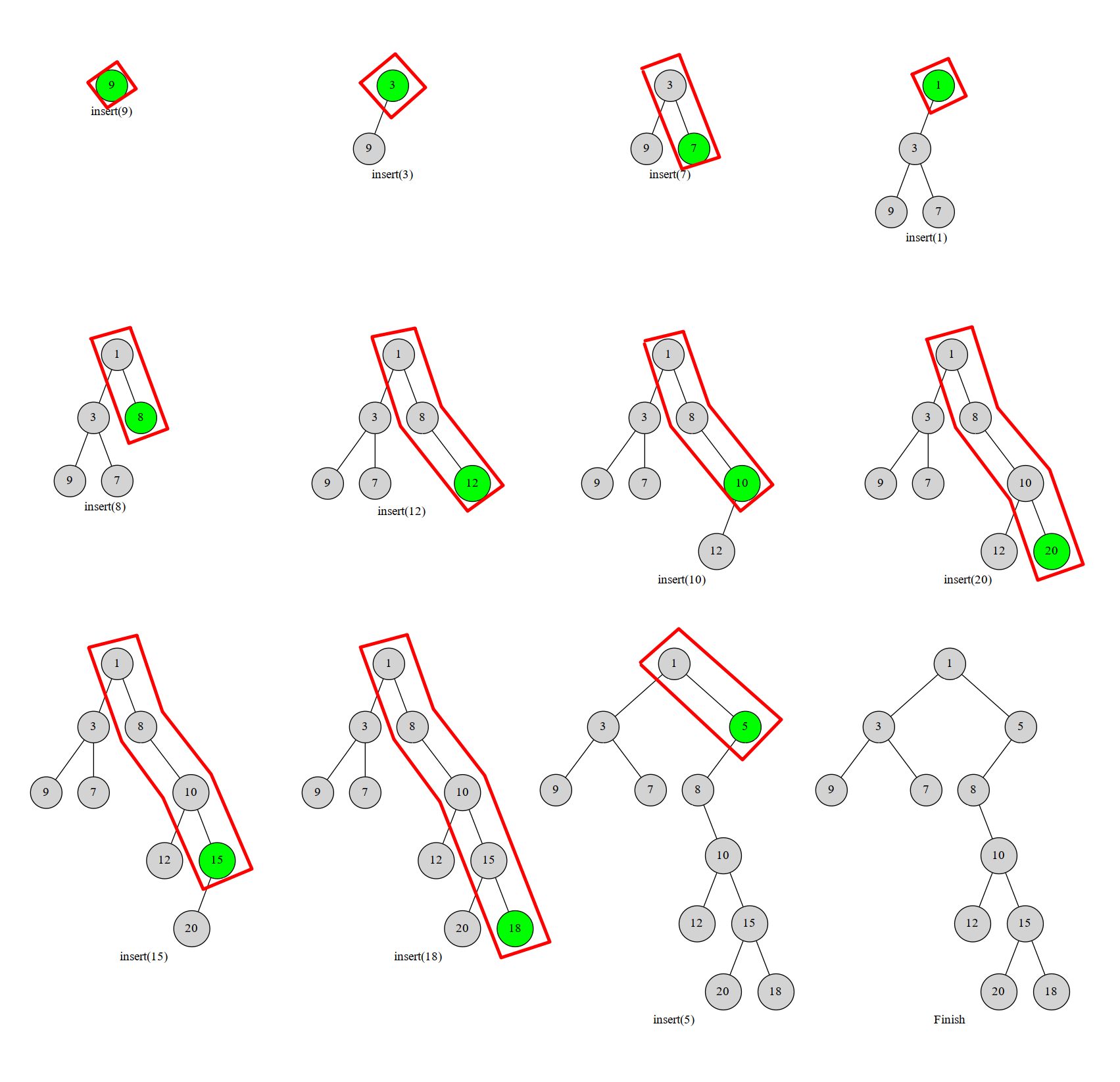
单调栈维护右链
可以发现,右链上的 $b$ 值单调不降。因此插入 $b_x$ 时,若 $b_y>b_x$,$y$ 一定不在新的右链里。
因此单调栈维护右链,即维护单调不降的序列,记录最后一个出栈的节点 $p$,$p$ 即为 $x$ 的左子节点。
每个节点至多入栈/出栈 $1$ 次,时间复杂度 $\mathcal O(n)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
vector<int>s;
for(int i=1;i<=n;i++){
int p=0;
while(s.size()&&b[s.back()]>b[i]){
p=s.back();
s.pop_back();
}
if(s.size()){
r[s.back()]=i;//记录右子节点
}
l[i]=p;//记录左子节点
s.push_back(i);
}
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
typedef long long ll;
constexpr const int N=1e7;
int n,p[N+1],l[N+1],r[N+1];
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>p[i];
}
vector
-
using namespace std;
typedef long long ll;
constexpr const int N=1e5;
int n,a[N+1],l[N+1],r[N+1];
void print(int p){
if(!p){
return;
}
cout<<p<<' ';
print(l[p]);
print(r[p]);
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
int x;
cin>>x;
a[x]=i;
}
vector