传统斜率优化 DP
给定正整数 $n,L$ 和数列 $a_1,a_2,a_3,\cdots,a_n$。$1\leq n\leq5\times10^4$。
将 $a$ 划分为 $k$ 段,设第 $i$ 段为 $a_{l_i},a_{l_i+1},\cdots,a_{r_i}$,则记 $\displaystyle x_i=r-l+\sum_{t=l}^ra_t$。
求最小值:
\[\sum_{i=1}^k\left(x_i-L\right)^2\]
显然可以 DP,设 $\textit{dp}_i$ 表示划分 $a_1\sim a_i$ 的最小代价。特别地,$\textit{dp}_0=0$。
记:
\[\textit{pre}_i=\sum_{j=1}^ia_j\]枚举 $i$ 所在段的左端点 $j$,有:
\[\textit{dp}_i=\min_{j=1}^i\left(\textit{dp}_{j-1}+(i-j+\textit{pre}_i-\textit{pre}_{j-1}-L)^2\right)\]答案为 $\textit{dp}_n$。时间复杂度:$\mathcal O\left(n^2\right)$,需要优化。
递推式的整理
考虑整理上面的递推式:
\[\begin{aligned} \textit{dp}_i&=\min_{j=1}^i\left(\textit{dp}_{j-1}+\left(i-j+\textit{pre}_i-\textit{pre}_{j-1}-L\right)^2\right)\\ &=\min_{j=0}^{i-1}\left(\textit{dp}_j+\left(i+\textit{pre}_i-j-\textit{pre}_j-L-1\right)^2\right)\\ &=\min_{j=0}^{i-1}\left(\textit{dp}_j+\left((i+\textit{pre}_i)-\left(j+\textit{pre}_j\right)-(L+1)\right)^2\right) \end{aligned}\]记 $f_i=i+\textit{pre}_i,L’=L+1$,有:
\[\begin{aligned} \textit{dp}_i&=\min_{j=0}^{i-1}\left(\textit{dp}_j+\left(f_i-L'-f_j\right)^2\right)\\ &=\min_{j=0}^{i-1}\left(\textit{dp}_j+(f_i-L')^2+f_j^2-2(f_i-L')f_j\right)\\ &=\min_{j=0}^{i-1}\left(\textit{dp}_j+f_j^2-2(f_i-L')f_j\right)+(f_i-L')^2\\ \end{aligned}\]考虑对于确定的 $i$,$f_i-L’$ 是定值。因此仅仅考虑与 $j$ 相关的部分:
\[\textit{dp}_j+f_j^2-2(f_i-L')f_j\]我们想高效地求出上式的最小值。
斜率转化
考虑决策点 $j_1,j_2$,钦定 $j_1<j_2$ 且 $j_1$ 优于 $j_2$,有:
\[\begin{aligned} \textit{dp}_{j_1}+f_{j_1}^2-2(f_i-L')f_{j_1}&\leq \textit{dp}_{j_2}+f_{j_2}^2-2(f_i-L')f_{j_2}\\ \textit{dp}_{j_1}+f_{j_1}^2-2(f_i-L')f_{j_1}&\leq \textit{dp}_{j_2}+f_{j_2}^2-2(f_i-L')f_{j_2}\\ -2(f_i-L')(f_{j_1}-f_{j_2})&\leq\textit{dp}_{j_2}+f_{j_2}^2-\left(\textit{dp}_{j_1}+f_{j_1}^2\right) \end{aligned}\]现在考虑 $f_{j_1}-f_{j_2}$ 的正负性,这影响到不等式的变号。发现钦定了 $0\leq j_1<j_2$,且题目中 $\textit{pre}i\geq 0$,因此有 $f{j_1}<f_{j_2}$,即 $f_{j_1}-f_{j_2}<0$。
故,有:
\[\begin{aligned} -2(f_i-L')&\geq\dfrac{\left(\textit{dp}_{j_2}+f_{j_2}^2\right)-\left(\textit{dp}_{j_1}+f_{j_1}^2\right)}{f_{j_1}-f_{j_2}}\\ 2(f_i-L')&\leq\dfrac{\left(\textit{dp}_{j_1}+f_{j_1}^2\right)-\left(\textit{dp}_{j_2}+f_{j_2}^2\right)}{f_{j_1}-f_{j_2}}\\ \end{aligned}\]在此情况下有 $j_1$ 优于 $j_2$。
观察不等式右边 $\dfrac{\left(\textit{dp}{j_1}+f{j_1}^2\right)-\left(\textit{dp}{j_2}+f{j_2}^2\right)}{f_{j_1}-f_{j_2}}$ 的形式,很像一个东西:
\[k=\dfrac{y_1-y_2}{x_1-x_2}\]即斜率。
决策点与凸包
因此对于每一个决策点 $j$,可以在平面直角坐标系内得到一个点:
\[A_j\left(f_j,\textit{dp}_j+f_j^2\right)\]在本文中,$A_i$ 一方面代表平面直角坐标系内由 $i$ 相关信息组成的点 $A_i$,另一方面代表决策点 $i$。
记 $x_i=2(f_i-L’)$,则决策点 $j_1$ 优于 $j_2$ 的条件重述为:
\[x_i\leq\dfrac{\left(\textit{dp}_{j_1}+f_{j_1}^2\right)-\left(\textit{dp}_{j_2}+f_{j_2}^2\right)}{f_{j_1}-f_{j_2}}\]记 $k_{i,j}$ 表示 $A_iA_j$ 的斜率,则可表述为:
\[x_i\leq k_{j_1,j_2}\]设三个点 $A_1,A_2,A_3$,如果出现了如图所示的情况,则有 $A_2$ 一定不是最优的。(即 $k_{2,3}\leq k_{1,2}$)
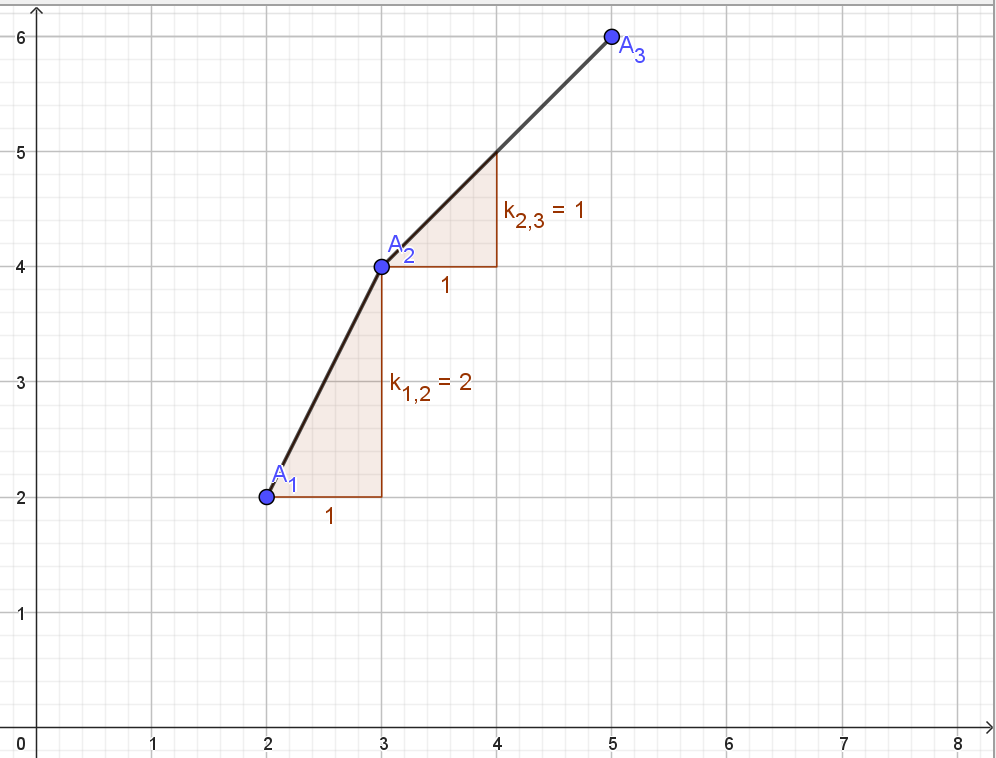
假设 $A_2$ 最优,则有:
\[x_i\leq k_{2,3}\]但是考虑到 $k_{2,3}\leq k_{1,2}$,则有 $x_i\leq k_{1,2}$。因此 $A_1$ 优于 $A_2$。故 $A_2$ 一定不是最优的。
这样就可以直接从平面直角坐标系中删去 $A_2A_3$ 这条线段,即删去 $A_2$,连接 $A_1A_3$。
最终得到的就是一堆线段,并且满足斜率单调不降。因此可以从中找到满足限制条件的最优决策点,并维护新的决策点 $A_i$,将 $A_i$ 加入平面直角坐标系。
这样的操作实际上也就是维护一个凸壳。所谓凸壳,在斜率优化中即各边斜率单调的图形(其实也可以称为「凸包」,但是不严谨)。如图所示便是一个下凸壳(斜率单调不降,也是本题所维护的):
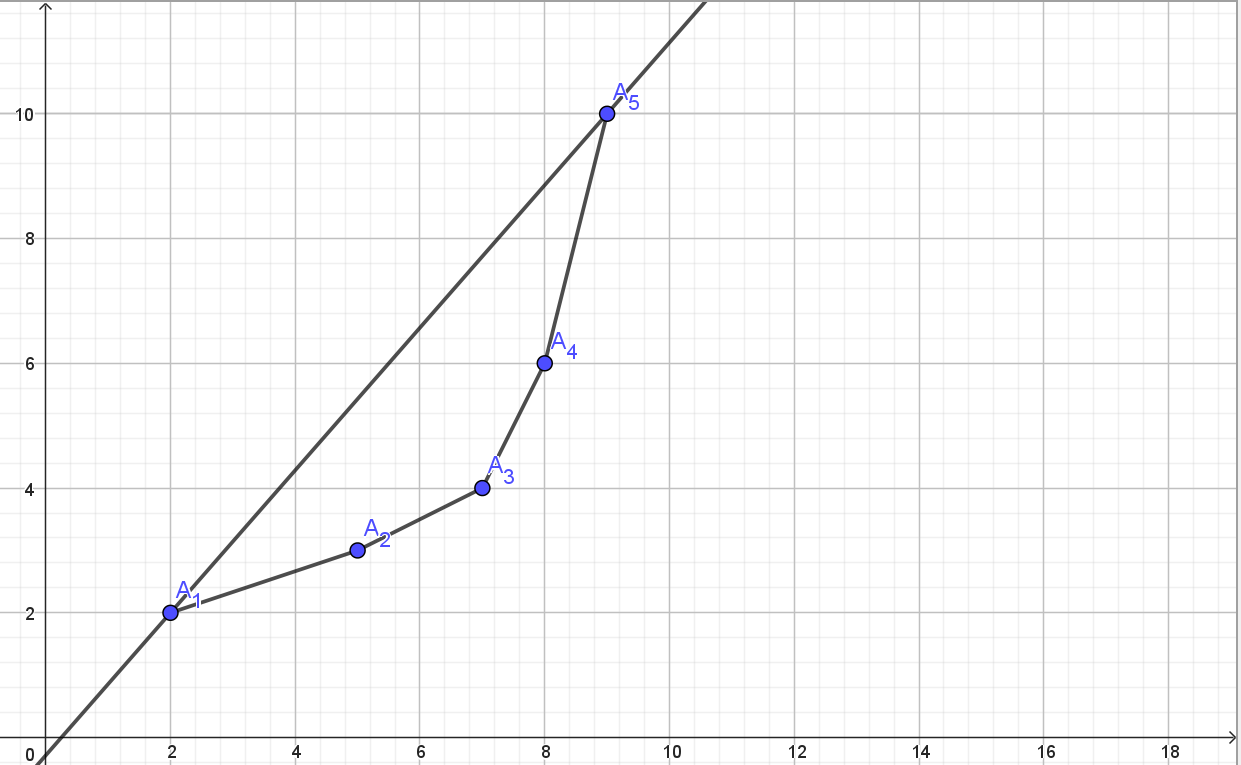
与之对应的还有上凸壳,即斜率单调不升。
实现步骤
考虑维护凸壳的具体步骤。使用一个栈来维护凸壳中的点。
-
寻找最优决策点。
-
使用最优决策点 $A_j$ 更新当前信息($\textit{dp}_i$)。
-
将 $A_i$ 作为新的决策点加入。
如果 $A_i$ 和栈顶 $A_x$ 构成的线段 $A_xA_i$ 满足 $A_x$ 一定不优,则将 $A_x$ 弹出。
当无法弹出时,加入 $A_i$。
寻找决策点
「寻找最优决策点」这一步一般会有两种方法,使用场景不同,复杂度也不同。
二分
凸壳中的斜率单调递增,因此可以二分。时间复杂度 $\mathcal O(\log n)$。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
typedef long long ll;
constexpr const int N=5e4;
int n,L,a[N+1];
ll pre[N+1],f[N+1],dp[N+1];
struct slopeDP{
struct node{
ll x,y;
int id;
}q[N+1];
int front,rear;
slopeDP(){
front=1;
rear=0;
}
double slope(node i,node j){
return (i.y-j.y)/(i.x-j.x);
}
void push(int id){
node x={f[id],dp[id]+f[id]*f[id],id};
while(front+1<=rear && slope(q[rear],x)<=slope(q[rear-1],q[rear])){
rear--;
}
q[++rear]=x;
}
int query(int x){
int l=front,r=rear-1,ans=rear;
while(l<=r){
int mid=l+r>>1;
if(slope(q[mid],q[mid+1])>=x){
ans=mid;
r=mid-1;
}else{
l=mid+1;
}
}
return q[ans].id;
}
}t;
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>L;
L++;
for(int i=1;i<=n;i++){
cin>>a[i];
pre[i]=pre[i-1]+a[i];
f[i]=i+pre[i];
}
t.push(0);
for(int i=1;i<=n;i++){
int j=t.query(2*(f[i]-L));
dp[i]=dp[j]+f[j]*f[j]-2*(f[i]-L)*f[j];
dp[i]+=(f[i]-L)*(f[i]-L);
t.push(i);
}
cout<<dp[n]<<'\n';
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
### 决策单调性
发现决策点 $i$ 的限制条件 $x_i$ 是**单调递增**的,而凸壳中的斜率也是**单调递增**的。因此可以维护指针来代替二分。
其实也就等价于双端队列维护凸壳。
指针移动的总复杂度为 $\mathcal O(n)$,均摊复杂度 $\mathcal O(1)$。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
typedef long long ll;
constexpr const int N=5e4;
int n,L,a[N+1];
ll pre[N+1],f[N+1],dp[N+1];
struct slopeDP{
struct node{
ll x,y;
int id;
}q[N+1];
int front,rear;
slopeDP(){
front=1;
rear=0;
}
double slope(node i,node j){
return (i.y-j.y)/(i.x-j.x);
}
void push(int id){
node x={f[id],dp[id]+f[id]*f[id],id};
while(front+1<=rear && slope(q[rear],x)<=slope(q[rear-1],q[rear])){
rear--;
}
q[++rear]=x;
}
int query(int x){
while(front+1<=rear && slope(q[front],q[front+1])<=x){
front++;
}
return q[front].id;
}
}t;
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>L;
L++;
for(int i=1;i<=n;i++){
cin>>a[i];
pre[i]=pre[i-1]+a[i];
f[i]=i+pre[i];
}
t.push(0);
for(int i=1;i<=n;i++){
int j=t.query(2*(f[i]-L));
dp[i]=dp[j]+f[j]*f[j]-2*(f[i]-L)*f[j];
dp[i]+=(f[i]-L)*(f[i]-L);
t.push(i);
}
cout<<dp[n]<<'\n';
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
# 斜率不单调的情况
> 现在考虑 $f_{j_1}-f_{j_2}$ 的**正负性**,这影响到**不等式的变号**。发现钦定了 $0\leq j_1<j_2$,且题目中 $\textit{pre}_i\geq 0$,因此有 $f_{j_1}<f_{j_2}$,即 $f_{j_1}-f_{j_2}<0$。
但是在有一些题目中,斜率并不单调,甚至于横坐标也不单调,这无法使用传统斜率优化解决。可以使用平衡树、
CDQ 分治等方法维护,此处给出一种基于**[李超线段树](./LiChao-Segment-Tree)**的方法。
***
> [例题:洛谷 P4027 [NOI2007] 货币兑换](https://www.luogu.com.cn/problem/P4027)。
>
> ***
>
> > 必然存在一种最优的买卖方案满足:每次买进操作使用完所有的人民币,每次卖出操作卖出所有的金券。
>
> 因此我们仅仅考虑这两种操作。
>
> 设 $\textit{dp}_i$ 为第 $i$ 天获得的**最多的钱**。特别地,钦定 $\textit{dp}_0=s$,为初始时拥有的钱。
>
> 记 $a_i,b_i$ 分别为第 $i$ 天 A 券、B 券的价值,$\textit{cntA}_i,\textit{cntB}_i$ 分别为第 $i$ 天用 $\textit{dp}_i$ 元买入的 A 券、B 券数量。则有:
>
> $$
> \begin{cases}
> \textit{cntA}_i\cdot a_i+\textit{cntB}_i\cdot b_i=\textit{dp}_i\\
> \dfrac{\textit{cntA}_i}{\textit{cntB}_i}=\textit{rate}_i
> \end{cases}
> $$
>
> 不难得到:
>
> $$
> \begin{aligned}
> \textit{cntA}_i&=\textit{rate}_i\cdot\textit{cntB}_i\\
> &=\dfrac{\textit{dp}_i\cdot\textit{rate}_i}{a_i\cdot\textit{rate}_i+b_i}\\
> \textit{cntB}_i&=\dfrac{\textit{dp}_i}{a_i\cdot\textit{rate}_i+b_i}
> \end{aligned}
> $$
>
> 因此可得转移:
>
> $$
> \textit{dp}_i=\max\left(\textit{dp}_{i-1},\max_{j=0}^{i-1}\left(\textit{cntA}_j\cdot a_i+\textit{cntB}_j\cdot b_i\right)\right)
> $$
>
>
> * 不卖出金券,为 $\textit{dp}_{i-1}$。
> * 卖出金券,枚举上一次买入金券的时间即可。
>
> ***
>
> $\textit{dp}_{i-1}$ 是好维护的,问题来到如何快速求得 $\max\limits_{j=0}^{i-1}\left(\textit{cntA}_j\cdot a_i+\textit{cntB}_j\cdot b_i\right)$。
考虑决策点 $j$ 的贡献 $\textit{cntA}_j\cdot a_i+\textit{cntB}_j\cdot b_i$。
李超线段树可以向坐标系内**添加一次函数**,并查询指定位置的最大值。李超线段树维护斜率优化 DP 同样如此。
$i$ 的信息是确定的,决策点 $j$ 的贡献可转化为:
$$
a_i\left(\textit{cnt}A_j+\textit{cntB}_j\cdot\dfrac{b_i}{a_i}\right)
$$
$a_i$ 确定,只需要考虑 $\textit{cnt}A_j+\textit{cntB}_j\cdot\dfrac{b_i}{a_i}$。但是 $\dfrac{b_i}{a_i}$ 此时为**定值**,可以很好的处理。
那么我们就**将其贡献转化为了一次函数 $y=kx+b$ 的形式**。决策点 $j$ 对应的一次函数为:
$$
y=\textit{cntB}_j\cdot x+\textit{cntA}_j
$$
决策点 $j$ 对于 $i$ 的贡献在 $x=\dfrac{b_i}{a_i}$ 处在李超线段树上查询最大值即可。
特别地,此处李超树维护的一次函数定义域为 $[-\infty,+\infty]$。正因此,修改复杂度为 $\mathcal O(\log n)$。
不要插入直线 $y=s$
即 $\textit{dp}_0$ 对应一次函数。
这会导致贡献算成 $a_is$。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
constexpr const int N=1e5+5;
constexpr const double eps=1e-9;
int n;
double a[N+1],b[N+1],rate[N+1];
double dp[N+1],cntA[N+1],cntB[N+1];
int len,pos[N+1+1];
double hashPos[N+1+1];
struct line{
double k,b;
line(double k=0,double b=0){
line::k=k;
line::b=b;
}
double operator ()(int x){
return k*hashPos[x]+b;
}
}line[N+1+1];
struct LiChaoSegTree{
struct node{
int l,r;
int id;
}t[(N+1)<<2|1];
void build(int p,int l,int r){
t[p]={l,r};
if(l==r){
return;
}
int mid=l+r>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
}
bool leq(double a,double b){
return a-b<-eps;
}
bool geq(double a,double b){
return a-b>eps;
}
bool eq(double a,double b){
return abs(a-b)<=eps;
}
bool check(int u,int v,int x){
double yU=line[u](x),yV=line[v](x);
return geq(yU,yV);
}
void down(int p,int x){
int &id=t[p].id;
if(t[p].l==t[p].r){
if(check(x,id,t[p].l)){
id=x;
}
return;
}
if(check(x,id,t[p<<1].r)){
swap(x,id);
}
if(check(x,id,t[p<<1].l)){
down(p<<1,x);
}
if(check(x,id,t[p<<1|1].r)){
down(p<<1|1,x);
}
}
double query(int p,int x){
double ans=line[t[p].id](x);
if(t[p].l==t[p].r){
return ans;
}
if(x<=t[p<<1].r){
ans=max(ans,query(p<<1,x));
}else{
ans=max(ans,query(p<<1|1,x));
}
return ans;
}
}t;
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>dp[0];
static double tmp[N+1+1];
for(int i=1;i<=n;i++){
cin>>a[i]>>b[i]>>rate[i];
hashPos[i]=b[i]/a[i];
tmp[i]=hashPos[i];
}
hashPos[n+1]=tmp[n+1]=0;
sort(hashPos+1,hashPos+n+2);
for(int i=1;i<=n;i++){
pos[i]=lower_bound(hashPos+1,hashPos+n+2,tmp[i])-hashPos;
}
t.build(1,1,n+1);
for(int i=1;i<=n;i++){
dp[i]=max(dp[i-1],a[i]*t.query(1,pos[i]));
cntB[i]=dp[i]/(a[i]*rate[i]+b[i]);
cntA[i]=rate[i]*cntB[i];
line[i]={cntB[i],cntA[i]};
t.down(1,i);
}
cout<<fixed<<setprecision(3)<<dp[n]<<'\n';
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>