持续更新中,对于较为简单的题目,会直接给出题解。对于较为复杂的题目,会给出核心摘要及详细题解的链接。
题目主要来源于[此处](https://www.luogu.com.cn/problem/list?type=luogu&page=1&tag=3,129,139,141,144,152,323,435,443,444,464 82,83 22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,58,59,60),以及一些没有 DP 标签但自认为与 DP 有较深的关系的题目。
NOIP2005
[NOIP 2005 普及组] 采药
经典 01 背包问题。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
int n,m,w[1001],c[1001],f[1001][1001];
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>w[i]>>c[i];
}
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
f[i][j]=f[i-1][j];
if(j>=w[i])f[i][j]=max(f[i][j],f[i-1][j-w[i]]+c[i]);
}
}
cout<<f[m][n]<<endl;
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
## [[NOIP 2005 提高组] 过河](https://www.luogu.com.cn/problem/P1052)
首先不难设计朴素 DP:设 $\textit{dp}_{i}$ 表示跳到坐标 $i$ 时的最小石子数量。
记 $\textit{flag}_{i}$ 表示坐标 $i$ 是否有石子,有:
$$
\textit{dp}_i=\min_{j=i-t}^{i-s}\textit{dp}_j+\textit{flag}_i
$$
注意到 $L\leq10^9$,会 MLE。因此考虑优化。发现 $1\leq s,t\leq10$,也许有一些性质可以利用。
令两个石子之间的距离为 $x$。
则若 $x>t(t-1)$,则 $x\iff t(t-1)$。由此可以 DP。
证明
不妨设步数仅有两种:$p,p+1$。
设 $p$ 走了 $x$ 步,$p+1$ 走了 $y$ 步。
设最终走到的点为 $z$,则有:
$$ px+(p+1)y=n $$
因为 $\gcd(p,p+1)=1$,由裴蜀定理,上述方程一定有整数解。
当 $0\leq x\leq p$ 时,有:
$$ y=\dfrac{m-px}{p+1}\geq\dfrac{m-p^2}{p+1}\geq\dfrac{p(p+1)-px-1}{p+1}\geq0 $$
因此,当 $m\geq p(p+1)$ 时,$p(p+1)$ 之后的点一定能走到。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
int l,s,t,m,f[10001],a[10001],flag[10001];
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%d",&l);
scanf("%d%d%d",&s,&t,&m);
for(int i=1;i<=m;i++)scanf("%d",a+i);
if(s==t){
int cnt=0;
for(int i=1;i<=m;i++)cnt+=((a[i]%s)==0);
printf("%d\n",cnt);
return 0;
}sort(a+1,a+m+1);
int pl=min(l-a[m],100);
for(int i=m;i>=1;i--)a[i]=min(a[i]-a[i-1],90);
l=0;
for(int i=1;i<=m;i++){
l+=a[i];
flag[l]=true;
}l+=pl;
for(int i=1;i<=l+t;i++){
f[i]=2147483646;
for(int j=s;j<=t;j++){
if(i>=j)f[i]=min(f[i],f[i-j]+flag[i]);
}
}
int Min=2147483647;
for(int i=l;i<=l+t;i++)Min=min(Min,f[i]);
printf("%d",Min);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
# NOIP2006
## [[NOIP 2006 普及组] 开心的金明](https://www.luogu.com.cn/problem/P1060)
经典完全背包问题。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
//v:价格,p:单个乘积,f:Dp数组
int n,m,v[25],p[25],f[25][30000];
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>v[i]>>p[i];
p[i]*=v[i];
}
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
f[i][j]=f[i-1][j];
if(j>v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+p[i]);
}
}
cout<<f[m][n]<<endl;
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
## [[NOIP 2006 提高组] 能量项链](https://www.luogu.com.cn/problem/P1063)
记 $L(i),R(i)$ 分别表示 $i$ 的前驱/后继。
记 $\textit{dp}_{l,r}$ 表示珠子 $l,l+1,\cdots,r$ 按照某种顺序合并的最大能量,则有:
$$
\textit{dp}_{l,r}=\max_{i=l}^r\left(\textit{dp}_{l,i}+a_la_{R(i)}a_{R(r)}+\textit{dp}_{i,r}\right)
$$
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
int n,a[101],s[101][101];
int L(int x){
if(x==1)return n;
return x-1;
}
int R(int x){
if(x==n)return 1;
return x+1;
}//[l,r]最大能量
int f(int l,int r){
if(s[l][r])return s[l][r];
int cnt=0;
for(int i=l;i!=r;i=R(i)){
cnt=max(cnt, f(l,i) + f(R(i),r) + a[l] * a[R(i)] * a[R(r)] );
}return s[l][r]=cnt;
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",a+i);
int ans=0;
for(int i=1;i<=n;i++)ans=max(ans,f(i,L(i)));//环
printf("%d\n",ans);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
## [[NOIP 2006 提高组] 金明的预算方案](https://www.luogu.com.cn/problem/P1064)
发现主件至多两个附件,因此可以分类讨论。
考虑 DP,设 $\textit{dp}_{i,j}$ 表示前 $i$ 个物品,花费为 $j$ 的答案。
附件的 DP 可以转移到主件上进行,一个主件的状态有:
* 只有主件。
* 主件和第一个附件。
* 主件和第二个附件。
* 主件和两个附件。
依此转移即可。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
constexpr const int N=3.2e4,M=60;
struct object{
int v,w;
pair<int,int>child;
bool main;
}a[M+1];
int n,m,dp[M+1][N+1];
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
int v,p,q;
cin>>v>>p>>q;
a[i].v=v;
a[i].w=p;
if(q){
if(!a[q].child.first){
a[q].child.first=i;
}else{
a[q].child.second=i;
}
a[i].main=false;
}else{
a[i].main=true;
}
}
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
dp[i][j]=dp[i-1][j];
int &first=a[i].child.first,&second=a[i].child.second;
if(!a[i].main){
continue;
}
if(j>=a[i].v){
dp[i][j]=max(dp[i][j],dp[i-1][j-a[i].v] + a[i].v*a[i].w);
}
if(j>=a[i].v+a[first].v){
dp[i][j]=max(dp[i][j],dp[i-1][j-a[i].v-a[first].v] + a[i].v*a[i].w + a[first].v*a[first].w);
}
if(second){
if(j>=a[i].v+a[second].v){
dp[i][j]=max(dp[i][j],dp[i-1][j-a[i].v-a[second].v] + a[i].v*a[i].w + a[second].v*a[second].w);
}
if(j>=a[i].v+a[first].v+a[second].v){
dp[i][j]=max(dp[i][j],
dp[i-1][j-a[i].v-a[first].v-a[second].v] + a[i].v*a[i].w + a[first].v*a[first].w + a[second].v*a[second].w
);
}
}
}
}
cout<<dp[m][n]<<'\n';
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
# NOIP2007
## [[NOIP 2007 普及组] 守望者的逃离](https://www.luogu.com.cn/problem/P1095)
贪心即可。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
long long m,s,t,run,fly;
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
cin>>m>>s>>t;
for(int i=1;i<=t;i++){
run+=17;//跑步17m/s
if(m>=10){
m-=10;
fly+=60;
}else m+=4;
run=max(run,fly);
if(run>=s){
cout<<"Yes"<<endl<<i<<endl;
return 0;
}
}cout<<"No"<<endl<<run<<endl;
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
## [[NOIP 2007 提高组] 矩阵取数游戏](https://www.luogu.com.cn/problem/P1005)
首先需要理解题意:
* 不同行之间是独立的。
* 设计一种方式,使得行内得分最大。
* 求所有行的得分之和。
考虑单独一行如何做。设 $\textit{dp}_{l,r}$ 表示取数取走 $a_l,a_{l+1},\cdots,a_r$ 时的最大得分。
则有:
$$
\textit{dp}_{l,r}=2\max\left(\textit{dp}_{l+1,r}+a_l,\textit{dp}_{l,r-1}+a_r\right)
$$
考虑第 $i$ 次取 $x$,$x$ 的贡献是 $2^ix$,即上式。因为每次乘 $2$,里面的数便相当于乘上 $2^{i'}$。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
typedef __int128 lll;
constexpr const int N=80,M=80;
int n,m,a[N+1][M+1];
lll f(int i,int l,int r){
static lll mem[N+1][N+1][N+1];
if(l<1||m<l||r<1||m<r||r<l){
return 0;
}
lll &ans=mem[i][l][r];
if(ans){
return ans;
}
return ans=2*max(f(i,l+1,r)+a[i][l],f(i,l,r-1)+a[i][r]);
}
template
证明
考虑 $i\sim j$ 的路径上一点 $l$,使得 $k\sim l$ 是 $k$ 至路径 $i\sim j$ 的接触点。则 $k$ 至 $i\sim j$ 路径的距离为 $\textit{dis}_{l,k}$。
那么注意到 $i\sim k$ 由 $i\sim l$ 和 $l\sim k$ 两部分组成,$j\sim k$ 同理。
则有:
$$ \begin{aligned} \textit{dis}_{i,k}&=\textit{dis}_{i,l}+\textit{dis}_{l,k}\\ \textit{dis}_{j,k}&=\textit{dis}_{j,l}+\textit{dis}_{l,k} \end{aligned} $$
$l$ 是不确定的,因此考虑消除 $l$,并直接求出 $\textit{dis}_{l,k}$。注意到 $\textit{dis}_{i,l}+\textit{dis}_{j,l}=\textit{dis}_{i,j}$,因此可以两式相加。
于是可以得到上式。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
constexpr const int N=300;
int n,s,dis[N+1][N+1];
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
memset(dis,0x3f,sizeof(dis));
cin>>n>>s;
for(int i=1;i<n;i++){
int u,v,w;
cin>>u>>v>>w;
dis[u][v]=dis[v][u]=w;
}
for(int k=1;k<=n;k++){
dis[k][k]=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
}
}
}
int ans=2147483647;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(dis[i][j]>s){
continue;
}
int Max=dis[i][1]+dis[j][1]-dis[i][j];
for(int k=2;k<=n;k++){
Max=max(Max,dis[i][k]+dis[j][k]-dis[i][j]);
}
ans=min(ans,Max>>1);
}
}
cout<<ans<<'\n';
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
# NOIP2008
## [[NOIP 2008 普及组] 传球游戏](https://www.luogu.com.cn/problem/P1057)
设计状态 $f_{i,j}$ 表示传球 $i$ 次,传球到 $j$ 的方案数,答案为 $f_{m,1}$。
不考虑边界,则有:
$$
f_{i,j}=f_{i-1,j-1}+f_{i-1,j+1}
$$
即从 $j-1,j+1$ 传球到 $j$。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
typedef long long ll;
ll n,m,f[31][31];
ll F(int i,int j){
if(j<1)return f[i][n];
if(j>n)return f[i][1];
return f[i][j];
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%lld %lld",&n,&m);
f[0][1]=1;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
f[i][j]=F(i-1,j-1)+F(i-1,j+1);
}
}printf("%lld\n",f[m][1]);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
## [[NOIP 2008 提高组] 传纸条](https://www.luogu.com.cn/problem/P1006)
设 $n$ 行 $m$ 列。
首先,这等效于从 $(1,1)$ 走两条道路到 $(n,m)$,并且一上一下,互不交叉。这也等效于从 $(1,2)$ 走一条到 $(n-1,m)$,从 $(2,1)$ 走一条到 $(n,m-1)$。
注意到 $2\leq n,m\leq50$,因此考虑一个高维 DP。
设 $\textit{dp}_{i_1,j_1,i_2,j_2}$ 表示从 $(1,2)$ 出发走到 $(i_1,j_1)$,从 $(2,1)$ 出发走到 $(i_2,j_2)$ 的最大合法和。
则有:
$$
\textit{dp}_{i_1,j_1,i_2,j_2}=\max\left(\textit{dp}_{i_1-1,j_1,i_2-1,j_2},\textit{dp}_{i_1-1,j_1,i_2,j_2-1},\textit{dp}_{i_1,j_1-1,i_2-1,j_2},\textit{dp}_{i_1,j_1-1,i_2,j_2-1}\right)+a_{i_1,j_1}+a_{i_2,j_2}
$$
需要注意的是,为了保证路径不交叉,有:
$$
i_1<i_2\\
j_1>j_2
$$
即时刻保证 $(i_1,j_1)$ 在 $(i_2,j_2)$ 的右上方。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
constexpr const int N=50,M=50;
int n,m,a[N+1][M+1],dp[N+1][M+1][N+1][M+1];
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
for(int i1=1;i1<=n;i1++){
for(int j1=1;j1<=m;j1++){
for(int i2=i1+1;i2<=n;i2++){
for(int j2=1;j2<j1;j2++){
dp[i1][j1][i2][j2]=max({
dp[i1-1][j1][i2-1][j2],
dp[i1-1][j1][i2][j2-1],
dp[i1][j1-1][i2-1][j2],
dp[i1][j1-1][i2][j2-1],
})+a[i1][j1]+a[i2][j2];
}
}
}
}
cout<<dp[n-1][m][n][m-1]<<'\n';
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
# NOIP2009
## [[NOIP 2009 普及组] 道路游戏](https://www.luogu.com.cn/problem/P1070)
记 $\textit{cost}_i$ 为在工厂 $i$ 购买机器人的费用,$a_{j,i}$ 为 $i$ 时刻,马路 $(j-1,j)$ 上的金币数。(实际上,是 $(j-1,j)$ 还是 $(j,j+1)$ 并不重要。)
考虑 DP 求解。
设 $\textit{dp}_{i,j,k}$ 表示在第 $i$ 时刻,走到 $j$,走了 $k$ 步的答案。
$k=0$ 则购买新机器人,从 $i-1$ 时刻的所有合法状态中找一个最大的相加即可。
$k\geq1$ 则从 $j-1$ 走一步即可。
则有:
$$
\textit{dp}_{i,j,k}=
\begin{cases}
\max\limits_{j'=1}^n\max\limits_{k'=0}^{\min(i-1,p)-1}\textit{dp}_{i-1,j',k'}-\textit{cost}_j+a_{j,i}
&k=0\\
\textit{dp}_{i-1,j-1,k-1}+a_{j,i}
&k\neq1
\end{cases}
$$
时间复杂度:$\mathcal O(nmp)$。
使用滚动数组优化即可做到空间复杂度 $\mathcal O(mp)$。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
constexpr const int N=1000,M=1000,P=M,inf=0x3f3f3f3f;
int n,m,p,a[N+1][M+1],cost[N+1];
int dp[2][N+1][P+1];
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m>>p;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
for(int i=1;i<=n;i++){
cin>>cost[i];
}
bool mode=0;
for(int i=1;i<=m;i++){
mode=!mode;
int Max;
if(i==1){
Max=0;
}else{
Max=-inf;
}
for(int j=1;j<=n;j++){
for(int k=0;k<i-1&&k<p;k++){
Max=max(Max,dp[!mode][j][k]);
}
}
for(int j=1;j<=n;j++){
dp[mode][j][0]=Max-cost[j]+a[j][i];
for(int k=1;k<i&&k<p;k++){
if(j==1){
dp[mode][j][k]=dp[!mode][n][k-1]+a[j][i];
}else{
dp[mode][j][k]=dp[!mode][j-1][k-1]+a[j][i];
}
}
}
}
int ans=dp[mode][1][0];
for(int i=1;i<=n;i++){
for(int j=0;j<m&&j<p;j++){
ans=max(ans,dp[mode][i][j]);
}
}
cout<<ans<<'\n';
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
## [[NOIP 2009 提高组] 最优贸易](https://www.luogu.com.cn/problem/P1073)
分为买入和卖出两步,考虑**分层图**。
第一层到第二层表示买入,权值为负;第二层到第三层表示卖出,权值为正。样例即:
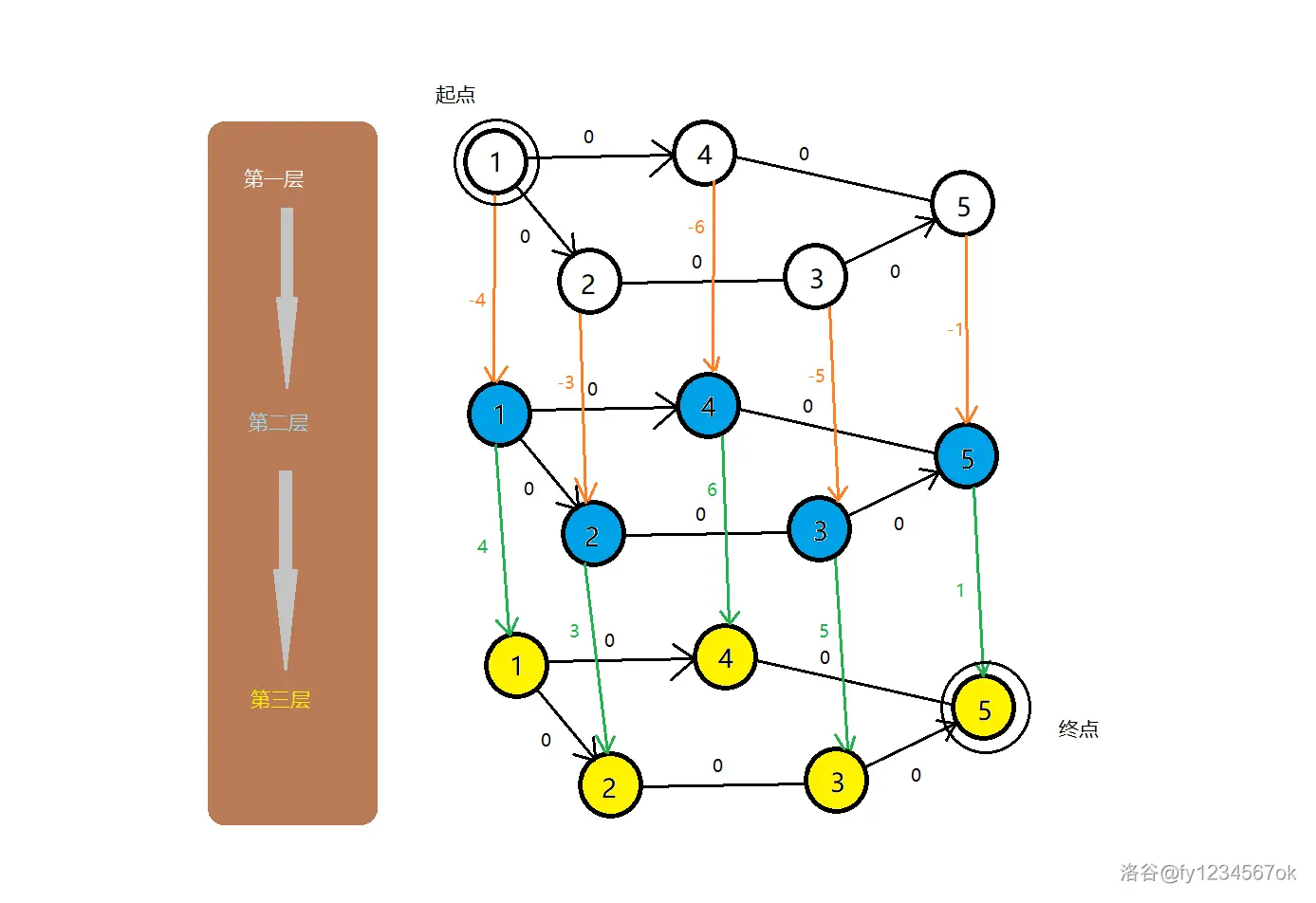
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
typedef long long ll;
constexpr const int N=100000,M=500000,Len=10000000;
int n,a[N+1];
vector<pair<int,int> >g[N*3+1];
int SPFA(int s,int t){
queue
进一步优化
注意到,必须有 $i=j_1+2j_2+3j_3+4j_4$,状态 $\textit{dp}_{i,j_1,j_2,j_3,j_4}$ 才是合法的。
那么 $i$ 这一维其实没什么用处,因为可以直接枚举 $j_1,j_2,j_3,j_4$ 来确定。
这样是 $\mathcal O\left(V^4\right)$ 的。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
constexpr const int N=350,M=120,V=40;
int n,m,a[N+1],cnt[V+1],dp[5][V+1][V+1][V+1][V+1];
inline int ask(int x){
x--;
x%=5;
if(x<0){
x+=5;
}
return x;
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=m;i++){
int x;
cin>>x;
cnt[x]++;
}
for(int i=1;i<=n;i++){
for(int j1=0;j1<=cnt[1] && j1<=i;j1++){
for(int j2=0;j2<=cnt[2] && j1+2*j2<=i;j2++){
for(int j3=0;j3<=cnt[3] && j1+2*j2+3*j3<=i;j3++){
for(int j4=0;j4<=cnt[4] && j1+2*j2+3*j3+4*j4<=i;j4++){
int Max=0;
if(j1>0&&i>1){
Max=max(Max,dp[ask(i-1)][j1-1][j2][j3][j4]);
}
if(j2>0&&i>2){
Max=max(Max,dp[ask(i-2)][j1][j2-1][j3][j4]);
}
if(j3>0&&i>3){
Max=max(Max,dp[ask(i-3)][j1][j2][j3-1][j4]);
}
if(j4>0&&i>4){
Max=max(Max,dp[ask(i-4)][j1][j2][j3][j4-1]);
}
dp[ask(i)][j1][j2][j3][j4]=Max+a[i];
}
}
}
}
}
cout<<dp[ask(n)][cnt[1]][cnt[2]][cnt[3]][cnt[4]]<<'\n';
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
## [[NOIP 2010 提高组] 引水入城](https://www.luogu.com.cn/problem/P1514)
发现不是很好求,考虑 DP。
容易发现中间都用处不大,重要的是第一行和最后一行,可以设 $\textit{dp}_{i,j}$ 表示处理到(不一定使用了)第一行前 $i$ 个格子,覆盖了最后一行前 $j$ 个格子的答案。
则有边界:
$$
\textit{dp}_{i,0}=0
$$
考虑如何递推。
设 $\textit{edge}_{i,j}$ 表示 $(1,i)$ 建造之后能否覆盖 $(n,j)$。这可以通过 $m$ 次 DFS 求出。同时可以求出是否存在 $(n,j)$ 不能被任何一个 $(1,i)$ 建造后覆盖,这就是**无解**。
有:
$$
\textit{dp}_{i,j}=\min\left(\textit{dp}_{i-1,j},\min_{k+1\sim j\text{ 都可以被覆盖}}\textit{dp}_{i-1,k}\right)
$$
形式化地来讲:
$$
\textit{dp}_{i,j}=\min\left(\textit{dp}_{i-1,j},\min_{k\in[0,j-1]\land\operatorname{check}(i,k+1,j)}\textit{dp}_{i-1,k}\right)
$$
其中:
$$
\operatorname{check}(i,k+1,j)=\left[0\not\in\set{\textit{edge}_{i,k+1},\textit{edge}_{i,k+2},\cdots,\textit{edge}_{i,j}}\right]
$$
在实际代码中,可以 $j-1\sim 0$ 枚举 $k$,使用 `break` 优化即可。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
constexpr const int N=500,M=500;
constexpr const int f[4][2]={ {0,1},{0,-1},{1,0},{-1,0} };
int n,m,a[N+1][M+1],dp[M+1][M+1];
bool edge[N+1][M+1],can[M+1];
bool vis[N+1][M+1];
void dfs(int i,int j,int s){
vis[i][j]=true;
if(i==n){
edge[s][j]=can[j]=true;
}
for(int k=0;k<4;k++){
int ii=i+f[k][0],jj=j+f[k][1];
if(1<=ii&&ii<=n&&1<=jj&&jj<=m && !vis[ii][jj] && a[i][j]>a[ii][jj]){
dfs(ii,jj,s);
}
}
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
for(int i=1;i<=m;i++){
memset(vis,0,sizeof(vis));
dfs(1,i,i);
}
int cnt=0;
for(int i=1;i<=m;i++){
if(!can[i]){
cnt++;
}
}
if(cnt){
cout<<"0\n"<<cnt<<'\n';
cout.flush();
return 0;
}
memset(dp,0x3f,sizeof(dp));
for(int i=0;i<=m;i++){
dp[i][0]=0;
}
for(int i=1;i<=m;i++){
for(int j=1;j<=m;j++){
dp[i][j]=dp[i-1][j];
for(int k=j-1;k>=0;k--){
if(!edge[i][k+1]){
break;
}
dp[i][j]=min(dp[i][j],dp[i-1][k]+1);
}
}
}
cout<<"1\n"<<dp[m][m]<<'\n';
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
# NOIP2011
## [[NOIP 2011 普及组] 表达式的值](https://www.luogu.com.cn/problem/P1310)
首先要明确两种运算的定义,用 $+$ 表示 `+`(题面中的 $\oplus$),用 $*$ 表示 `*`(题面中的 $\times$)。
则有:
| $+$ | $*$ |
| :-----: | :-----: |
| $0+0=0$ | $0*0=0$ |
| $0+1=1$ | $0*1=0$ |
| $1+0=1$ | $1*0=0$ |
| $1+1=1$ | $1*1=1$ |
对于诸如此类的关于表达式的问题,有两种做法:
* 转前/后缀表达式,栈模拟。
* 转「表达式树」,做树上问题。
对于此题,就可以转**表达式树**后进行树上 DP。
所谓表达式树,即以「实际运算的运算符」为节点(即不包括括号)建二叉树。
运算符间存在优先级的问题,一个子树便代表一个运算结果。即,将原表达式拆分为 $A\circ B$ 的形式,$A,B$ 便是 $\circ$ 的左、右子树运算结果。
$\mathcal O\left(n^2\right)$ 的建树是简单的,即 $[l,r]$ 建成一个树时,找 $x$ 使得 $x$ 对应的是一个**括号之外**的运算符。如果有 $+$ 最好,否则 $*$ 次之。这样可以保证 $+,*$ 之间的运算优先级。特别地,若两端都是括号且配对,则直接建 $[l+1,r-1]$。
但是也存在 $\mathcal O(n)$ 的建树方法:
* 建笛卡尔树。
* ST 表先 $\mathcal O(n\log n)$ 预处理每一个点的优先级的区间最小值,建树时 $x$ 即 $[l,r]$ 内优先级最小的点的位置。
具体而言,`(` 和 `)` 的优先级为 $+\infty$。对于 `+` 和 `*`,令包裹其括号层数为 $k$,则 `+` 为 $2k$,`*` 为 $2k+1$。
即被括号包裹一定不优。
***
树形 DP,设 $\textit{dp}_{x,0},\textit{dp}_{x,1}$ 分别表示 $x$ 子树运算结果为 $0,1$ 时的方案数。
根据运算规则 DP 即可。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
constexpr const int N=100000,P=10007,inf=0x3f3f3f3f;
int n;
char a[N+1];
struct expTree{
static int root;
struct node{
char op;
int lChild,rChild;
}t[N<<1|1];
void print(int x=root){
if(!x){
return;
}
print(t[x].lChild);
cerr<<t[x].op<<' ';
print(t[x].rChild);
}
struct sparseTable{
int st[N+1][__lg(N+1)+1],rest[N+1][__lg(N+1)+1];
void build(){
int k=0;
for(int i=1;i<=n;i++){
if(a[i]=='('){
k++;
st[i][0]=inf;
}else if(a[i]==')'){
k--;
st[i][0]=inf;
}else if(a[i]=='+'){
st[i][0]=k<<1;
}else{
st[i][0]=k<<1|1;
}
rest[i][0]=i;
}
for(int i=1;(1<<i)<=n;i++){
for(int x=1;x+(1<<i)-1<=n;x++){
if(st[x][i-1]<=st[x+(1<<i-1)][i-1]){
st[x][i]=st[x][i-1];
rest[x][i]=rest[x][i-1];
}else{
st[x][i]=st[x+(1<<i-1)][i-1];
rest[x][i]=rest[x+(1<<i-1)][i-1];
}
}
}
}
int query(int l,int r){
int s=__lg(r-l+1);
if(st[l][s]<st[r-(1<<s)+1][s]){
return rest[l][s];
}else{
return rest[r-(1<<s)+1][s];
}
}
}st;
int match[N+1];
void pre(){
vector
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
constexpr const int N=100,M=100,P=1e6+7;
int n,m,a[N+1],dp[N+1][M+1];
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
dp[0][0]=1;
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){
for(int k=0;k<=a[i]&&k<=j;k++){
dp[i][j]=(dp[i][j]+dp[i-1][j-k])%P;
}
}
}
cout<<dp[n][m]<<'\n';
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
# NOIP2013
## [[NOIP 2013 普及组] 小朋友的数字](https://www.luogu.com.cn/problem/P1982)
最大子段和问题。
记数字为 $\textit{num}_i$,特征值为 $a_i$,分数为 $f_i$。
则有:
$$
\begin{aligned}
a_i&=\max_{1\leq l\leq r\leq i}\sum_{j=l}^r\textit{num}_j\\
&=\max\left(a_{i-1}+\textit{num}_i,a_{i-1}\right)\\
f_i&=
\begin{cases}
a_1&i=1\\
\max\left(f_{i-1},f_{i-1}+\max\limits_{j=1}^{i-1}a_j\right)&i>1
\end{cases}
\end{aligned}
$$
答案为 $\max\limits_{i=1}^nf_i\bmod p$。$\mathcal O(n)$ 计算。
参考代码
```cpp //#include<bits/stdc++.h> #include-
using namespace std;
typedef __int128 lll;
typedef long long ll;
constexpr const int N=1e6;
int n,P;
ll a[N+1];
lll f[N+1];
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>P;
f[0]=-(1ll<<62);
for(int i=1;i<=n;i++){
cin>>a[i];
a[i]=max(a[i-1]+a[i],a[i]);
f[i]=max(f[i-1],(lll)a[i]);
}
lll pl=f[1]+a[1],ans=f[1];
for(int i=2;i<=n;i++){
ans=max(ans,pl);
pl=max(pl,pl+f[i]);
}
cout<<(int)(ans%P)<<'\n';
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
```
</details>
## [[NOIP 2013 提高组] 花匠](https://www.luogu.com.cn/problem/P1970)
显然,最后剩下的花的高度 $g_1,g_2,g_3,\cdots,g_m$ 需要满足下列性质任意一条:
* $g_1