题目传送门

题意分析

树上问题

首先，$n$ 个点 $n-1$ 条边，显然是一个树。

因此，$\operatorname{dist}(i,j)$ 其实可以 $\mathcal O(1)$ 计算出来。只需要 $\mathcal O(n\log n)$ 预处理一个 DFS 序 LCA 即可。（详见此处）

斯特林数

对于整数 $x$ 的 $k$ 次方，其实可以通过第二类斯特林数展开：

\[\begin{aligned} x^k&=\sum_{i=0}^k\begin{Bmatrix}k\\i\end{Bmatrix}x^{\underline{i}}\\ &=\sum_{i=0}^k\begin{Bmatrix}k\\i\end{Bmatrix}i!\dbinom{x}{i}\\ \end{aligned}\]

因此，$S(u)$ 就可以转化为：

\[\begin{aligned} S(u)&=\sum_{v=1}^n\operatorname{dist}(u,v)^k\\ &=\sum_{v=1}^n\sum_{i=0}^k\begin{Bmatrix}k\\i\end{Bmatrix}i!\dbinom{\operatorname{dist}(u,v)}{i}\\ &=\sum_{i=0}^k\begin{Bmatrix}k\\i\end{Bmatrix}i!\sum_{v=1}^n\dbinom{\operatorname{dist}(u,v)}{i} \end{aligned}\]

树形 DP

不难发现，关键便在于对于每一个点 $u$，求出 $\sum\limits_{v=1}^n\dbinom{\operatorname{dist}(u,v)}{i}$，且 $0\leq i\leq k$。

如果 $u$ 确定，其实很简单，只需要 DFS 一遍即可。但是需要对于每一个点 $u$ 都求一次，暴力 DFS 的复杂度是 $\mathcal O\left(n^2\right)$ 的，无法接受。

不难发现，设边 $(x,y)$，且 $x$ 为 $y$ 的父节点，则将树根从 $x$ 变为 $y$ 是会且仅会影响 $x,y$ 的答案的。因此考虑换根 DP。

第一次 DP

设 $\textit{dp}{x,i}$ 表示节点 $x$ 的子树内，$i=i$ 时的 $\sum\limits{y=1}^n\dbinom{\operatorname{dist}(x,y)}{i}$。

记 $\textit{son}_x$ 表示 $x$ 的子节点集。

显然，有：

\[\begin{aligned} \textit{dp}_{x,0}&=\sum_{y\in\textit{son}_x}\textit{dp}_{y,0}+1\\ \textit{dp}_{x,i}&=\sum_{y\in\textit{son}_x}\left(\textit{dp}_{y,i}+\textit{dp}_{y,i-1}\right) \end{aligned}\]

$i=0$ 时，无论 $\operatorname{dist}(x,y)$ 取何值，总有 $\dbinom{\operatorname{dist}(x,y)}{0}=1$。因此，$\textit{dp}_{x,0}$ 就是 $x$ 子树内节点个数，包括自己。
$i\neq0$ 时，考虑组合数递推公式：
\[\dbinom{\operatorname{dist}(x,y)}{i}=\dbinom{\operatorname{dist}(x,y)-1}{i}+\dbinom{\operatorname{dist}(x,y)-1}{i-1}\]
$\operatorname{dist}(x,y)-1$，即对应从 $y$ 开始。因为 $y$ 对应的是 $y$ 的子树中的贡献，$x$ 走进去必然经过长度为 $1$ 的 $(x,y)$。

故，有：
\[\textit{dp}_{x,i}=\textit{dp}_{y,i}+\textit{dp}_{y,i-1}\]

换根 DP

设根节点 $x$ 为 $y$ 的父节点，已知 $\textit{dp}{x,i}$，推出 $y$ 为根节点时的 $\textit{dp}{y,i}$。

如图：

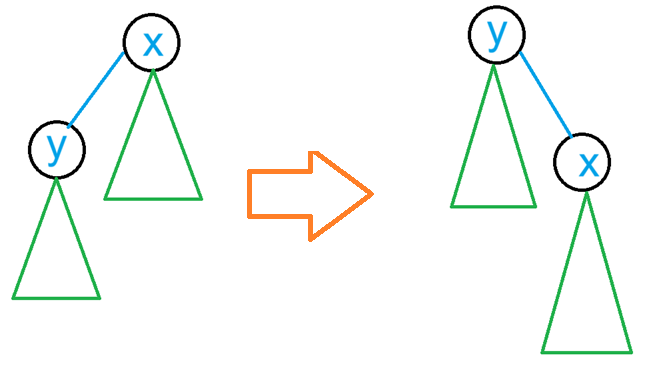
首先，要求出 $x$ 作为根节点 $y$ 的子节点时的子树内的 $\textit{dp}’_{x,i}$。

只需要减去 $y$ 对 $x$ 的贡献即可。

即：

\[\begin{aligned} \textit{dp}'_{x,0}&=\textit{dp}_{x,0}-\textit{dp}_{y,0}\\ \textit{dp}'_{x,i}&=\textit{dp}_{x,i}-(\textit{dp}_{y,i}+\textit{dp}_{y,i-1}) \end{aligned}\]

这时，想求出根节点 $y$ 的 $\textit{dp}’{y,i}$，只需要加上对应的 $\textit{dp}’{x,i}$ 即可：

\[\begin{aligned} \textit{dp}'_{y,0}&=\textit{dp}_{y,0}+\textit{dp}'_{x,0}\\ \textit{dp}'_{y,i}&=\textit{dp}_{y,i}+(\textit{dp}'_{x,i}+\textit{dp}'_{x,i-1}) \end{aligned}\]

这样，我们就将根节点从 $x$ 换成了 $y$，这时 $\mathcal O(k)$ 统计答案即可。

AC 代码

注意答案非负。

时间复杂度：$\mathcal O\left(n\log n+nk+n\right)$。

其中，$\mathcal O(nk)$ 是为了计算组合数、第二类斯特林数。

//#include<bits/stdc++.h>
#include<algorithm> 
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=5e4,K=150,P=10007;
int n,k,ans[N+1];
vector<int>g[N+1];
namespace base{
	int dfn[N+1],order[N+1],dep[N+1],father[N+1],st[N+1][__lg(N+1)+1],reSt[N+1][__lg(N+1)+1];
	void dfs(int x,int fx){
		father[x]=fx;
		dep[x]=dep[fx]+1;
		static int cnt;
		dfn[x]=++cnt;
		order[dfn[x]]=x;
		for(int i:g[x]){
			if(i==fx){
				continue;
			}
			dfs(i,x);
		}
	}
	int qpow(int base,int n){
		int ans=1;
		while(n){
			if(n&1){
				ans=1ll*ans*base%P;
			}
			base=1ll*base*base%P;
			n>>=1;
		}
		return ans;
	}
	int fact[K+1];
	void pre(){
		fact[0]=1;
		for(int i=1;i<=K;i++){
			fact[i]=1ll*fact[i-1]*i%P;
		}
		dfs(1,0);
		for(int i=1;i<=n;i++){
			st[i][0]=dep[order[i]];
			reSt[i][0]=order[i];
		}
		for(int i=1;(1<<i)<=n;i++){
			for(int x=1;x+(1<<i)-1<=n;x++){
				if(st[x][i-1]<st[x+(1<<i-1)][i-1]){
					st[x][i]=st[x][i-1];
					reSt[x][i]=reSt[x][i-1];
				}else{
					st[x][i]=st[x+(1<<i-1)][i-1];
					reSt[x][i]=reSt[x+(1<<i-1)][i-1];
				}
			}
		}
	}
	int lca(int u,int v){
		if(u==v){
			return u;
		}
		if(dfn[u]>dfn[v]){
			swap(u,v);
		}
		int s=__lg(dfn[v]-dfn[u]);
		if(st[dfn[u]+1][s]<st[dfn[v]-(1<<s)+1][s]){
			return father[reSt[dfn[u]+1][s]];
		}else{
			return father[reSt[dfn[v]-(1<<s)+1][s]];
		}
	}
	int dist(int u,int v){
		int lcaUV=lca(u,v);
		return dep[u]+dep[v]-2*dep[lcaUV];
	}
	int C(int n,int m){
		if(n<0||m<0||n<m){
			return 0;
		}
		static int mem[N+1][K+1];
		if(!m){
			return 1;
		}
		if(mem[n][m]){
			return mem[n][m];
		}
		return mem[n][m]=C(n-1,m)+C(n-1,m-1);
	}
	int Stirling2(int n,int k){
		static int mem[K+1][K+1];
		if(n<0||k<0||n<k){
			return 0;
		}
		if(!k){
			return !n;
		}
		if(mem[n][k]){
			return mem[n][k];
		}
		return mem[n][k]=(Stirling2(n-1,k-1)+1ll*k*Stirling2(n-1,k)%P)%P;
	} 

}
namespace DP{
	int dp[N+1][K+1];
	void dfs0(int x,int fx){
		dp[x][0]=1;
		for(int y:g[x]){
			if(y==fx){
				continue;
			}
			dfs0(y,x);
			dp[x][0]=(1ll*dp[x][0]+dp[y][0])%P;
			for(int i=1;i<=k;i++){
				dp[x][i]=(1ll*dp[x][i]+dp[y][i]+dp[y][i-1])%P;
			}
		}
	}
	void dfs1(int x,int fx){
		for(int i=0;i<=k;i++){
			ans[x]=(1ll*ans[x]+1ll*dp[x][i]*base::Stirling2(k,i)%P*base::fact[i]%P)%P;
			if(ans[x]<0){
				ans[x]+=P;
			}
		}
		for(int y:g[x]){
			if(y==fx){
				continue;
			}
			
			dp[x][0]=(dp[x][0]-dp[y][0])%P;
			for(int i=1;i<=k;i++){
				dp[x][i]=(dp[x][i]-dp[y][i]-dp[y][i-1])%P;
			}
			
			dp[y][0]=(dp[y][0]+dp[x][0])%P;
			for(int i=1;i<=k;i++){
				dp[y][i]=(dp[y][i]+dp[x][i]+dp[x][i-1])%P;
			}
			
			dfs1(y,x);
			
			dp[y][0]=(dp[y][0]-dp[x][0])%P;
			for(int i=1;i<=k;i++){
				dp[y][i]=(dp[y][i]-dp[x][i]-dp[x][i-1])%P;
			}
			
			dp[x][0]=(dp[x][0]+dp[y][0])%P;
			for(int i=1;i<=k;i++){
				dp[x][i]=(dp[x][i]+dp[y][i]+dp[y][i-1])%P;
			}
		}
	}
	int main(){
		dfs0(1,0);
		dfs1(1,0);
		return 0;
	}
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	cin>>n>>k;
	for(int i=1;i<n;i++){
		int u,v;
		cin>>u>>v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	base::pre();
	DP::main();
	for(int i=1;i<=n;i++){
		cout<<ans[i]<<'\n';
	}
	
	cout.flush(); 
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

题解：[集训队互测 2011] Crash 的文明世界

洛谷P4827 | 斯特林数展开下降幂 | 换根 DP