双栈模拟队列
本篇题解主要介绍本题线性做法所利用的数据结构。
时间限制 $\text{300ms}$,又是交互题(无需 IO),显然是为了卡时间。
那么这道题大概率是一个 $\mathcal O(n)$ 的线性做法。
其实这道题目需要用到一个黑科技:双栈模拟队列。(具体见下文)
这道题目 DP 之后便是要维护一个数据结构,实现:
- 双端插入、删除。
- 查询最小值。
双端插入、删除使用双端队列即可,但是双端队列不能查询最小值。因为最小值不可差分,也就是说将最小值弹出后无法更新最小值。
于是考虑使用其他数据结构。
考虑到,前/后缀最小值是很好维护的。弹出元素时,可以利用其他前/后缀的信息来维护,插入时同样如此。
那么就考虑将我们需要维护的数据结构拆为两个能够维护前后缀最值的数据结构,从而维护最值。
如图:
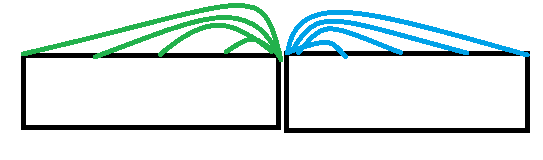
图中的线就是表示维护一个前/后缀最值。那么查询最值时,左右两端取最小即可。
如何实现双端插入、删除呢?这两个数据结构都需要实现这种功能。但是发现它们靠在一起的一端不会需要这种操作,因此“单端操作”,即栈。
那么思路就很清晰了,维护双栈模拟双端队列,同时维护前/后缀最值构成的区间最值。
但还是有一个小问题:要是在某一刻,一个栈中的元素弹空了,还要弹出怎么办?
这在普通数据结构的正常情况下是不会出现的,但是在这里会。因为有一些元素在另一个栈里。
这种时候,我们直接 $\mathcal O(\textit{size})$ 暴力重构即可,其中 $\textit{size}$ 表示此时双栈中元素的个数。
假定某一次 $\mathcal O(\textit{size}_0)$ 重构后,双栈中的元素个数为 $\textit{size}_0$,那么左右两个栈里元素个数均为 $\mathcal O\left(\dfrac{\textit{size}_0}2\right)$。
而在下一次重构前,至少需要弹出 $\mathcal O\left(\dfrac{\textit{size}_0}2\right)$ 个元素(弹空)。
那么就可以将重构操作的复杂度均摊到弹出操作上,两个操作的复杂度均摊下来都是 $\mathcal O(1)$ 的。
因此总复杂度仍为线性。
AC 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <bits/stdc++.h>
#define Mod 1000000007
#define getchar() ((p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2))?EOF:*p1++)
using namespace std;
namespace DS{
long long mn1[2500010],mn2[2500010];
long long num1[2500010],num2[2500010];
int top1,top2;
void init()
{
mn1[0]=mn2[0]=0x3f3f3f3f3f3f3f3f;
}
long long qry(){return min(mn1[top1],mn2[top2]);}
void ins(long long x){num1[++top1]=x;mn1[top1]=min(mn1[top1-1],x);}
void del1()
{
if(top1==0)
{
int hf=(top2+1)>>1;
top1=hf;
for(int i=1;i<=hf;i++) mn1[i]=min(mn1[i-1],num1[i]=num2[hf+1-i]);
top2-=hf;
for(int i=1;i<=top2;i++) mn2[i]=min(mn2[i-1],num2[i]=num2[i+hf]);
}
top1--;
if(top1==0)
{
int hf=top2>>1;
top1=hf;
for(int i=1;i<=hf;i++) mn1[i]=min(mn1[i-1],num1[i]=num2[hf+1-i]);
top2-=hf;
for(int i=1;i<=top2;i++) mn2[i]=min(mn2[i-1],num2[i]=num2[i+hf]);
}
}
void del2()
{
if(top2==0)
{
int hf=(top1+1)>>1;
top2=hf;
for(int i=1;i<=hf;i++) mn2[i]=min(mn2[i-1],num2[i]=num1[hf+1-i]);
top1-=hf;
for(int i=1;i<=top1;i++) mn1[i]=min(mn1[i-1],num1[i]=num1[i+hf]);
}
top2--;
if(top2==0)
{
int hf=top1>>1;
top2=hf;
for(int i=1;i<=hf;i++) mn2[i]=min(mn2[i-1],num2[i]=num1[hf+1-i]);
top1-=hf;
for(int i=1;i<=top1;i++) mn1[i]=min(mn1[i-1],num1[i]=num1[i+hf]);
}
}
}
int n,k,stk[2500010],s[2500010],rea,top,ans;
long long f[2500010];
int solve(int n,int k,int s[]){
for(int i=n+1;i>0;i--){
s[i]=s[i-1];
}
DS::init();
for(int i=1;i<=n;i++)
{
while(rea<=top&&s[stk[top]]<=s[i])
{
if(rea<top) DS::del1();
top--;
}
while(rea<=top&&stk[rea]<i-k)
{
if(rea<top) DS::del2();
rea++;
}
if(rea<=top) DS::ins(f[stk[top]]+s[i]);
stk[++top]=i;
f[i]=min(DS::qry(),f[max(0,i-k)]+s[stk[rea]]);
}
for(int i=n,bas=1;i;i--)
{
ans=(ans+f[i]%Mod*bas)%Mod;
bas=23ll*bas%Mod;
}
return ans;
}