可持久化线段树/主席树
可持久化线段树与主席树
“主席树”其实只是一个称呼,“主席树”的提出者也没有进行一个严谨的定义,一般主席树就是指可持久化权值线段树。
算法简介
可持久化线段树,可以维护多个历史版本下的线段树,支持单点修改,因此可以用来实现可持久化数组。
但是如果给每一个版本都开一个线段树,若有 $n$ 个节点,$m$ 个版本,空间复杂度就是 $\mathcal O(nm)$ 的,不能接受。
因此就有了可持久化线段树,通过一些手段避免了如此之高的空间复杂度,而能使空间复杂度变为 $\mathcal O\left(n+m\log n\right)$。
基本原理
假如我们已经有了一棵线段树:
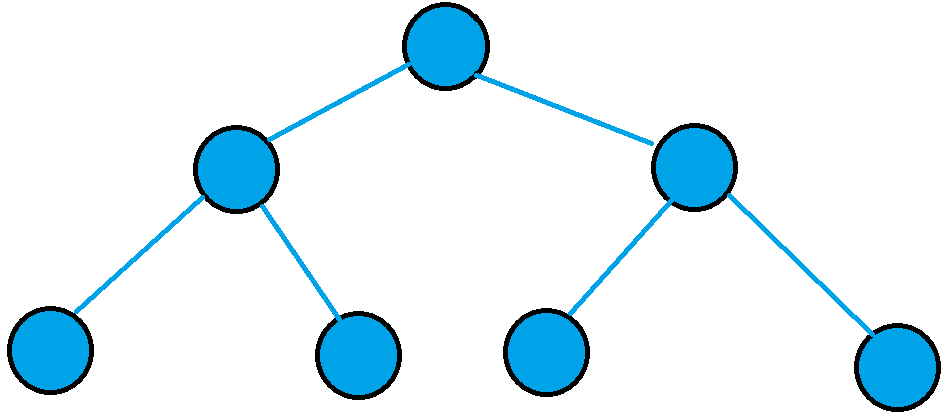
那么,以对最左侧的节点修改为例,修改成如图:
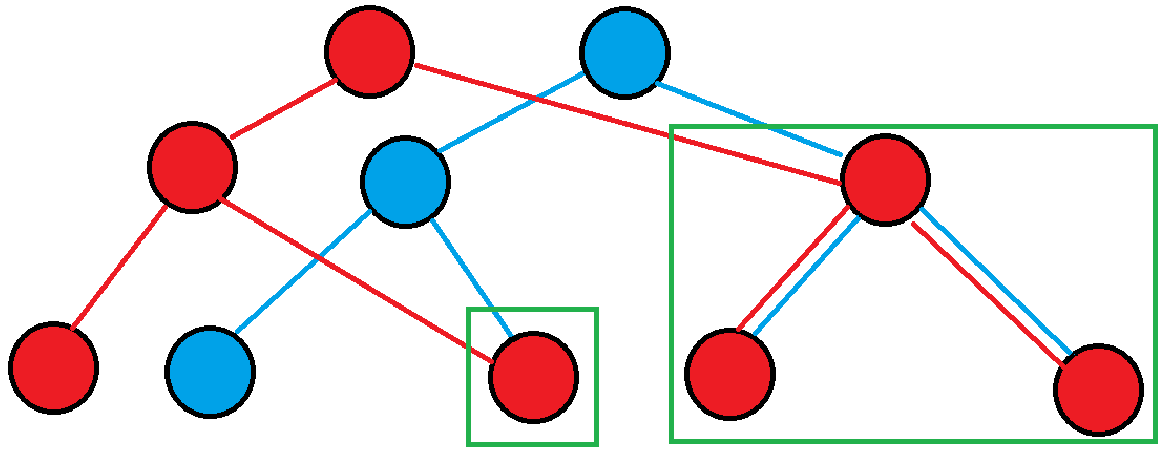
修改之后的树(红色部分)中显然并不是所有节点都修改了,图中绿色框出的部分没有任何修改。
事实上,修改一个叶节点会且仅会修改其祖先节点,因为有且仅有其祖先节点维护的信息包含了叶节点的信息。
那么修改时,需要复制的节点就是树的高度,即 $\left\lceil\log n\right\rceil+1$。
对于不需要复制的节点,可以直接连边。上图中的树可以简化为:
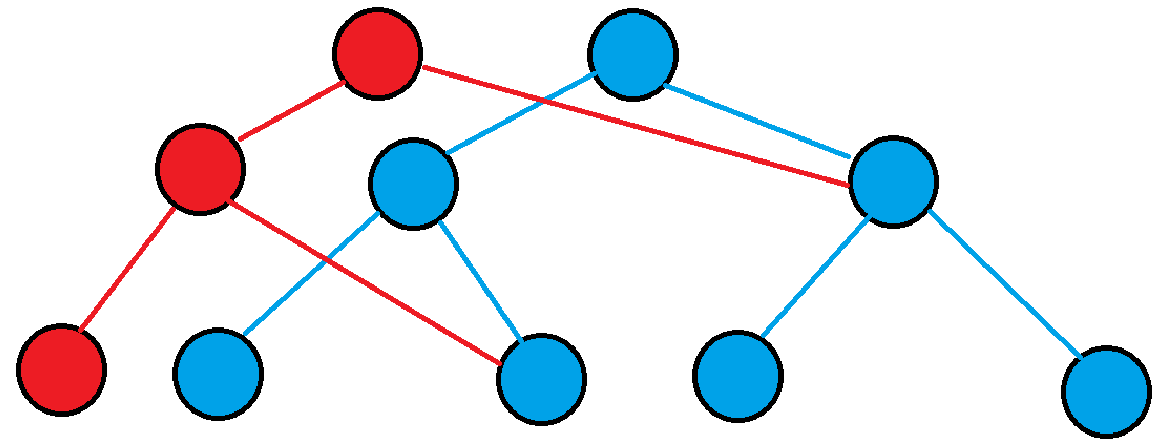
这样,我们访问某一个版本时,从对应版本的根节点开始查询即可,单个节点无需存储其版本号,因为每一个根节点都可以视作对应一棵独立的线段树。
与普通线段树的区别
可持久化线段树必须动态开点,否则不能实现“连边”。
代码实现
以例题要求实现可持久化数组为例。
单个节点
那么就是对于每一个叶节点,维护其对应的数组中的值。
1
2
3
4
struct node{
int value;
int l,r,lChild,rChild;
}t[4*N+M*(int)(ceil(log2(N))+1)+1];
其实节点数组的大小可以开大一些,保证不 MLE 即可。但是个人喜欢卡空间提前算好,不要学我。(4*N+M*(ceil(log2(N))+1) 即 $4n+m\left(\left\lceil\log n\right\rceil+1\right)$,初次建好 $\mathcal O(4n)$ 的线段树后,$m$ 次操作每次至多新增 $\mathcal O(\log n+1)$ 个节点。)
其中,$l,r$ 表示其维护的是区间 $[l,r]$ 的信息,$\textit{value}$ 是叶节点的值,$\textit{lChild},\textit{rChild}$ 分别是左子节点、右子节点。
线段树的两种写法,如果采用动态计算区间边界的写法,则无需 $l,r$。
根存储
使用数组存储即可。
1
int root[M+1];
root[i] 表示版本 $i$ 的根节点,至多 $m$ 个版本。
新建节点
新建节点(返回节点编号):
1
2
3
4
int create(node x){
t[++size]=x;
return size;
}
这种写法相较于直接将节点信息作为参数传入函数,有一个好处:可以在传参时使用列表,更为方便。
例如:
1
create({12,0,0});
除此之外,因为涉及到复制节点的操作,也可以封装一个函数:
1
2
3
4
int clone(int p){
t[++size]=t[p];
return size;
}
初始建树
和动态开点线段树基本一样。
建树函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
int build(int l,int r){
node x;
x.l=l,x.r=r;
if(l==r){
//这一块视需求而定,在本题中如此。
x.value=a[l];
return create(x);
}
int mid=l+r>>1;
x.lChild=build(l,mid);
x.rChild=build(mid+1,r);
return create(x);
}
build 函数返回的是建出来的树的根节点,调用时需要存储 root[0]。
即:
1
t.root[0]=t.build(1,n);
单点更新
其实没有必要找到对应的叶节点后再去一个一个复制其祖先节点——这样不光常数更大,而且不好实现(需要实现找父节点)。
只需要从根节点一路复制节点,复制到叶节点即可。
将 $a_x$ 更改为 $k$,返回修改后的(子)树根,代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//a[x]=k
int update(int p,int x,int k){
p=clone(p);//复制祖先节点
if(t[p].l==t[p].r){
t[p].value=k;
return p;
}
//更新&连边
if(x<=t[t[p].lChild].r){
t[p].lChild=update(t[p].lChild,x,k);
}else{
t[p].rChild=update(t[p].rChild,x,k);
}
return p;
}
为了实现将新建版本 $i$,将版本 $v$ 中的 $a_p$ 修改为 $c$,可以封装函数:
1
2
3
void update(int v,int i,int x,int k){
root[i]=update(root[v],x,k);
}
单点查询
单点查询更简单,直接找即可:
1
2
3
4
5
6
7
8
9
10
int query(int p,int x){
if(t[p].l==t[p].r){
return t[p].value;
}
if(x<=t[t[p].lChild].r){
return query(t[p].lChild,x);
}else{
return query(t[p].rChild,x);
}
}
同时,加上查询版本 $v$(这是新建版本 $i$,一般查询操作视为新建一个一样的版本):
1
2
3
4
5
//查询版本 v 的 a[p]
int query(int v,int i,int x){
root[i]=root[v];
return query(root[i],x);
}
例题 AC 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=1e6,M=1e6;
int a[N+1];
//个人喜欢封装,也建议封装,除非是需要卡常
struct segTree{
int root[M+1],size;
struct node{
int value;
int l,r,lChild,rChild;
}t[4*N+M*(int)(ceil(log2(N))+1)+1];
int create(node x){
t[++size]=x;
return size;
}
int clone(int p){
t[++size]=t[p];
return size;
}
int build(int l,int r){
node x;
x.l=l,x.r=r;
if(l==r){
x.value=a[l];
return create(x);
}
int mid=l+r>>1;
x.lChild=build(l,mid);
x.rChild=build(mid+1,r);
return create(x);
}
//a[x]=k
int update(int p,int x,int k){
p=clone(p);
if(t[p].l==t[p].r){
t[p].value=k;
return p;
}
if(x<=t[t[p].lChild].r){
t[p].lChild=update(t[p].lChild,x,k);
}else{
t[p].rChild=update(t[p].rChild,x,k);
}
return p;
}
void update(int v,int i,int x,int k){
root[i]=update(root[v],x,k);
}
int query(int p,int x){
if(t[p].l==t[p].r){
return t[p].value;
}
if(x<=t[t[p].lChild].r){
return query(t[p].lChild,x);
}else{
return query(t[p].rChild,x);
}
}
//版本 v 的 a[p]
int query(int v,int i,int x){
root[i]=root[v];
return query(root[i],x);
}
}t;
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
t.root[0]=t.build(1,n);
for(int i=1;i<=m;i++){
int v,op,p,c;
cin>>v>>op>>p;
switch(op){
case 1:
cin>>c;
t.update(v,i,p,c);
break;
case 2:
cout<<t.query(v,i,p)<<'\n';
break;
}
}
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
/*
5 1
59 46 14 87 41
0 2 1
59
*/
总结
其实,可持久化线段树的核心就是:复制根节点至修改节点路径上的所有节点,充分利用未修改的旧版本信息。
只要弄清楚这一点,那么可持久化线段树便很好理解了。
实际上还可以拓展到区间操作,也是类似地复制路径上节点,复杂度同为 $\mathcal O\left(\log n\right)$。因为访问到的节点都是普通线段树区间操作需要访问的节点,复制是 $\mathcal O(1)$ 的。