题意分析
给定序列 $a$,求 $a_l\sim a_r$ 的众数(出现次数最多的数)。
首先注意到 $1\leq a_i\leq10^9$,而 $n\leq4\times10^4$,显然可以离散化。
暴力会超时,那就优化暴力:对 $a$ 以 $\sqrt n$ 为块长进行分块,第 $i$ 块为 $a_{(i-1)\sqrt n+1}\sim a_{i\sqrt n}$。
既然题目要维护众数,那么分块也维护众数:记 $\textit{most}_{i,j}$ 表示第 $i$ 块至第 $j$ 块的众数。
求出 \(\textit{most}_{i,j}\) 是 $\mathcal O(n\sqrt n)$ 的:可以 $\mathcal O(\sqrt n)$ 枚举一个 $i$,随后在 $\mathcal O(n)$ 的时间内求出 \(\textit{most}_{i,1}\sim\textit{most}_{i,\sqrt n}\)。
那么,对于一次询问的 $l,r$,如图所示:
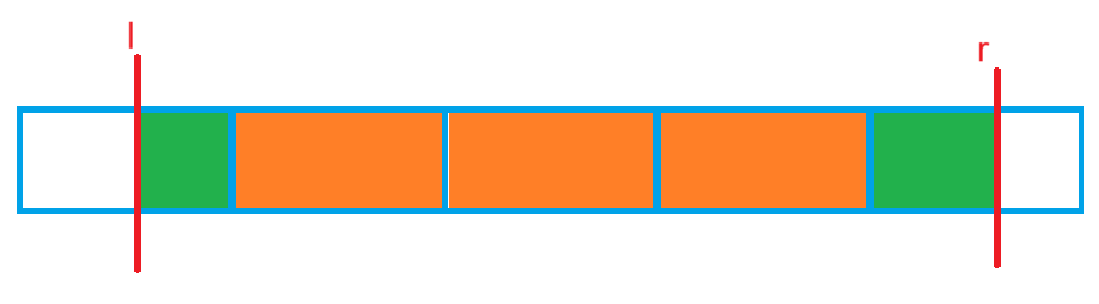
$a_l\sim a_r$ 的众数,显然就是图中橙色部分的众数,或绿色部分中可能的数。
记 $l$ 所在块为 $\textit{pl}$,$r$ 所在块为 $pr$。
-
$pr-pl\leq1$ 时,直接 $\mathcal O(\sqrt n)$ 扫一遍统计答案即可。
由于只有 $\mathcal O(\sqrt n)$ 个数,因此最多是 $\mathcal O(\sqrt n)$ 种颜色,不需要大小为 $\mathcal O(n)$ 的桶。
可以考虑哈希(
unordered_map)。 -
$pr-pl\geq2$ 时,橙色部分众数即 $\textit{most}_{pl+1,pr-1}$。
之后同上类似地 $\mathcal O(\sqrt n)$ 扫一遍绿色部分,统计出其中数 $x_i$ 的出现次数 $y_i$。
但是我们还不知道 $x_i$ 能否成为众数,因此需要先知道橙色部分里 $x_i$ 的出现次数。
这也可以维护。
记 $\textit{cnt}_{i,j}$ 表示前 $i$ 个块中 $j$ 的出现次数,则可以在预处理的时候先 $\mathcal O(n\sqrt n)$ 求出第 $i$ 个块中 $j$ 的出现次数,再 $\mathcal O(n\sqrt n)$ 做一次前缀和即可。
这时我们就知道了橙色部分 $x_i$ 的出现次数为:
\[\textit{cnt}_{\textit{pr}-1,x_i}-\textit{cnt}_{\textit{pl},x_i}+y_i\]于是可以判断 $x_i$ 是否为众数。
AC 代码
时间复杂度:$\mathcal O(n\sqrt n)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
#include<unordered_map>
using namespace std;
constexpr const int N=40000,M=50000,A=1e9,sqrtN=sqrt(N);
int n,m,a[N+1],tmp[N+1];
int len,size,cnt[sqrtN+1][N+1],most[sqrtN+1][sqrtN+1];
int pos(int x){
return ceil(1.0*x/len);
}
int edgeL(int x){
return (x-1)*len+1;
}
int edgeR(int x){
return x*len;
}
void pre(){
for(int i=1;i<=n;i++){
tmp[i]=a[i];
}
sort(tmp+1,tmp+n+1);
int m=unique(tmp+1,tmp+n+1)-tmp-1;
for(int i=1;i<=n;i++){
a[i]=lower_bound(tmp+1,tmp+m+1,a[i])-tmp;
}
len=sqrt(n);
for(int l=1,r=l+len-1;r<=n;l+=len,r+=len){
size++;
for(int j=l;j<=r;j++){
cnt[size][a[j]]++;
}
}
for(int i=1;i<=size;i++){
for(int j=1;j<=n;j++){
cnt[i][j]+=cnt[i-1][j];
}
}
for(int i=1;i<=size;i++){
unordered_map<int,int>count;
int Max=-1,u=-1;
for(int j=i;j<=size;j++){
for(int k=edgeL(j);k<=edgeR(j);k++){
int &pl=++count[a[k]];
if(pl>Max){
Max=pl;
u=a[k];
}else if(pl==Max){
u=min(u,a[k]);
}
}
most[i][j]=u;
}
}
}
int query(int l,int r){
int pl=pos(l),pr=pos(r);
if(pr-pl<=1){
unordered_map<int,int>count;
for(int i=l;i<=r;i++){
count[a[i]]++;
}
int Max=-1,ans=2147483647;
for(auto i:count){
if(i.second>Max){
Max=i.second;
ans=i.first;
}else if(i.second==Max){
ans=min(ans,i.first);
}
}
return tmp[ans];
}else{
unordered_map<int,int>count;
for(int i=l;i<=edgeR(pl);i++){
count[a[i]]++;
}
for(int i=edgeL(pr);i<=r;i++){
count[a[i]]++;
}
int ans=most[pl+1][pr-1],Max=cnt[pr-1][ans]-cnt[pl][ans];
for(auto i:count){
int x=i.first,y=i.second+cnt[pr-1][x]-cnt[pl][x];
if(y>Max){
Max=y;
ans=x;
}else if(y==Max){
ans=min(ans,x);
}
}
return tmp[ans];
}
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
bool flag=true;
for(int i=1;i<=n;i++){
cin>>a[i];
}
pre();
int ans=0;
while(m--){
int l0,r0,l,r;
cin>>l0>>r0;
l=(l0+ans-1)%n+1,r=(r0+ans-1)%n+1;
if(l>r){
swap(l,r);
}
ans=query(l,r);
cout<<ans<<'\n';
}
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}