参考资料 参考 Blog 参考资料

矩阵

简介

矩阵源于线性方程组，例如对于以下方程组：

\[\begin{cases} x_1+2x_2-x_3&=2\\ 2x_1+x_2+x_3&=7\\ -x_1+3x_2&=5 \end{cases}\]

将未知数分开，可以写为矩阵：

\[\begin{bmatrix} 1&2&-1\\ 2&1&1\\ -1&3&0 \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3 \end{bmatrix} = \begin{bmatrix} 2\\7\\5 \end{bmatrix}\]

由 $n$ 行 $m$ 列共计 $mn$ 个 $a_{i,j}$ 组成的数表 \(\begin{matrix}a_{1,1}&a_{1,2}&\cdots&a_{1,m}\\a_{2,1}&a_{2,2}&\cdots&a_{1,m}\\\vdots&\vdots&\ddots&\vdots\\a_{n,1}&a_{n,2}&\cdots&a_{n,m}\end{matrix}\) 被称为 $n$ 行 $m$ 列的矩阵，记为 $n\times m$ 矩阵。为表示这是一个整体，可以使用中括号括起，并使用大写字母表示：

\[A=\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots&a_{1,m}\\a_{2,1}&a_{2,2}&\cdots&a_{1,m}\\\vdots&\vdots&\ddots&\vdots\\a_{n,1}&a_{n,2}&\cdots&a_{n,m}\end{bmatrix}\]

这 $n\times m$ 个数被称为矩阵 $A$ 的元素，简称元。第 $i$ 行第 $j$ 列的元素可以记为 $A_{i,j}$。

• 若 $n=m$，可以称 $A$ 为 $n$ 阶方阵，OI 中大多数矩阵都是方阵（如行列式及其应用）。
• 对于一个方阵：
  • 若只有主对角线上有 $1$，其余均为 $0$，称其为单位矩阵，记为 $E$ 或 $I$。
  • 若只有主对角线上有非 $0$ 的值，其余均为 $0$，称其为对角矩阵。
  • 若主对角线下方均为 $0$，称为上三角矩阵；若主对角线上方均为 $0$，称为下三角矩阵。
• 若矩阵只有一行，称为行矩阵或行向量。
• 若矩阵只有一列，称为列矩阵或列向量。

矩阵运算

设矩阵 $A,B$。令 $A$ 是一个 $n_A\times m_A$ 的矩阵，$B$ 是一个 $n_B\times m_B$ 的矩阵。

矩阵加减

矩阵 $A,B$ 可以作加减运算，当且仅当 $n_A=n_B,m_A=m_B$。

令 $C=A\pm B$，则有：

\[C_{i,j}=A_{i,j}\pm B_{i,j}\]

矩阵数乘

设数 $k$，令 $C=k\times A$，则有：

\[C_{i,j}=kA_{i,j}\]

矩阵乘法

矩阵 $A,B$ 能够作乘法，当且仅当 $m_A=n_B$。

令 $C=A\times B$，则有：

\[C_{i,j}=\sum_{k=1}^{m_A}A_{i,k}B_{k,j}\]

参考代码

矩阵运算律

矩阵 $A,B$ 满足：

\[\begin{aligned} (AB)\times C&=A\times(B\times C)\\ A(B+C)&=A\times B+A\times C\\ \end{aligned}\]

即，矩阵满足乘法结合律与乘法分配律。但是，矩阵 不一定 满足乘法交换律。

考虑矩阵 $A,B$，可以计算 $A\times B=C$，但是 $B\times A=C$ 不一定成立。甚至于 $B\times A$ 可能都没有意义。

矩阵的逆

设方阵 $A,B$，满足 $A\times B=I$，记 $B=A^{-1}$ 为 $A$ 的逆矩阵。

$A^{-1}$ 存在当且仅当 $\vert A\vert\neq0$。$\vert A\vert$ 表示 $A$ 的行列式。

考虑将 $A$ 进行若干次变换从而得到 $I$，这些变换等价于让 $A$ 乘上 $A^{-1}$。

那么，确定了一个矩阵 $X$，只要对 $X$ 进行这些已经固定的变换，等价于让 $X$ 乘上 $A^{-1}$。

因此，从 $I$ 开始进行这些变换，即可得到 $I\times A^{-1}=A^{-1}$。

注：这里的变换指代的是类似于高斯消元法的初等变换。

例题链接

参考代码

行列式

行列式是对于一个方阵（行、列大小相同的矩阵）的一种运算，是研究线性方程组的一种工具。

方阵 $A$ 的行列式记作 $\det A$ 或 $\vert A\vert,\det(A)$。

引入

行列式的概念是在解线性方程组时提出的。

二阶行列式

已知二元线性方程组： \(\begin{cases} a_{1,1}x_1+a_{1,2}x_2=b_1\\ a_{2,1}x_1+a_{2,2}x_2=b_2 \end{cases}\)

角标的歧义

有些地方的角标不是形如“$a_{1,1}$”，而是“$a_{11}$”。这种写法在没有歧义的情况下也是可以的。

然而比如说对于 $a_{121}$，那么就无法分辨是第 $1$ 行第 $21$ 个还是第 $12$ 行第 $1$ 个，因此需要逗号分隔。

本文中为了严谨，全部使用逗号分隔。

解方程得到：

\[\begin{cases} x_1=\dfrac{b_1a_{2,2}-a_{1,2}b_2}{a_{1,1}a_{2,2}-a_{1,2}a_{2,1}}\\ x_2=\dfrac{b_2a_{1,1}-a_{2,1}b_1}{a_{1,1}a_{2,2}-a_{1,2}a_{2,1}}\\ \end{cases}\]

令 $D=a_{1,1}a_{2,2}-a_{1,2}a_{2,1}$。

可以发现，当 $D\neq0$ 时，方程组有唯一解，否则有无数解或无解。

可以发现，两个未知数 $x_1,x_2$ 的最终形式都是以 $D$ 为分母的分数。

实际上，在线性代数中，行列式的值是否为 $0$ 甚至比行列式的具体值更重要。

将方程组的系数拿出来，做成一个方阵，求其行列式为：

\[D= \begin{vmatrix} a_{1,1}&a_{1,2}\\ a_{2,1}&a_{2,2} \end{vmatrix} =a_{1,1}a_{2,2}-a_{1,2}a_{2,1}\]

行列式的 $\KaTeX$ 输入

使用 $\KaTeX$ 环境 vmatrix 即可。

$\det$ 可以使用 \det。

事实上，对于二阶行列式，其值为主对角线上元素之积减去副对角线上元素之积。

三阶行列式

设方阵：

\[\begin{matrix} a_{1,1}&a_{1,2}&a_{1,3}\\ a_{2,1}&a_{2,2}&a_{2,3}\\ a_{3,1}&a_{3,2}&a_{3,3} \end{matrix}\]

同样地解方程可得，其行列式为：

\[\begin{aligned} &\ \ \ \ \begin{vmatrix} a_{1,1}&a_{1,2}&a_{1,3}\\ a_{2,1}&a_{2,2}&a_{2,3}\\ a_{3,1}&a_{3,2}&a_{3,3} \end{vmatrix}\\ &=a_{1,1}a_{2,2}a_{3,3}+a_{1,2}a_{2,3}a_{3,1}+a_{1,3}a_{2,1}a_{3,2}-a_{3,1}a_{2,2}a_{1,3}-a_{2,1}a_{1,2}a_{3,3}-a_{1,1}a_{3,2}a_{2,3}\\ \end{aligned}\]

对角线法则

如图，红色实线部分冠以正号，蓝色虚线部分被冠以负号：

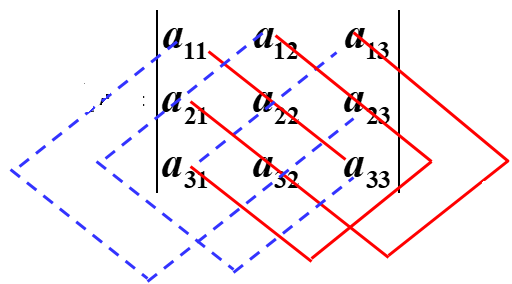
三阶行列式可以依照此图或上述公式计算。

例题

计算行列式：

\[\begin{vmatrix} 1&2&-4\\ -2&2&1\\\ -3&4&2 \end{vmatrix}\]

答案解析

由对角线法则，原行列式值为：$-14$。

解方程：

\[\begin{vmatrix} x+1&2&-1\\ 2&x+1&1\\ -1&1&x+1 \end{vmatrix} =0\]

答案解析

由三阶行列式，有：

$$ (x+1)^3+2\times1\times(-1)+(-1)\times2\times1-(-1)^2(x+1)-2^2(x+1)-1^2(x+1)=0 $$

解得 $x=-3$ 或 $x=\pm\sqrt3$。

行列式的逆序数定义

也称作“逆序对定义”、“全排列定义”等。

三阶行列式

观察三阶行列式：

\[\begin{aligned} &\ \ \ \ \begin{vmatrix} a_{1,1}&a_{1,2}&a_{1,3}\\ a_{2,1}&a_{2,2}&a_{2,3}\\ a_{3,1}&a_{3,2}&a_{3,3} \end{vmatrix}\\ &=a_{1,1}a_{2,2}a_{3,3}+a_{1,2}a_{2,3}a_{3,1}+a_{1,3}a_{2,1}a_{3,2}-a_{3,1}a_{2,2}a_{1,3}-a_{2,1}a_{1,2}a_{3,3}-a_{1,1}a_{3,2}a_{2,3}\\ \end{aligned}\]

可以发现：

• 三阶行列式共有 $6=3!$ 项。

• 每一项均为不同行且不同列的 $3$ 个元素的乘积。

  即：不考虑正负号，每一项均可写作 $a_{1,p_1}a_{2,p_2}a_{3,p_3}$，且 $\langle p_1,p_2,p_3\rangle$ 是一个 $1\sim3$ 的排列。

• 当 $\langle p_1,p_2,p_3\rangle$ 是偶排列的时候，对应项冠以正号。

• 当 $\langle p_1,p_2,p_3\rangle$ 是奇排列的时候，对应项冠以正号。

奇、偶排列

一个排列，若其逆序对个数为偶数，称其为偶排列；否则为奇排列。

记 $\tau(p_1,p_2,p_3)$ 为排列 $\langle p_1,p_2,p_3\rangle$ 的逆序对个数（有时也记作 $t(p_1,p_2,p_3)$），则 $3$ 阶行列式可写作：

\[\begin{vmatrix} a_{1,1}&a_{1,2}&a_{1,3}\\ a_{2,1}&a_{2,2}&a_{2,3}\\ a_{3,1}&a_{3,2}&a_{3,3} \end{vmatrix} =\sum_{\langle p_1,p_2,p_3\rangle}(-1)^{\tau(p_1,p_2,p_3)}a_{1,p_1}a_{2,p_2}a_{3,p_3}\]

其中，$\sum\limits_{\langle p_1,p_2,p_3\rangle}$ 表示对 $\lbrace 1,2,3\rbrace$ 的所有排列求和。

$\tau$ 的 $\KaTeX$ 输入

使用 \tau 即可。

推广到一般

对于 $n$ 阶行列式，有：

\[\begin{aligned} D&= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\\ &=\sum_{\langle p_1,p_2\cdots,p_n\rangle}(-1)^{\tau(p_1,p_2\cdots,p_n)}a_{1,p_1}a_{2,p_2}a_{3,p_3}\cdots a_{n,p_n} \end{aligned}\]

事实上，这也是行列式的定义式。下文中所有的“定义式”，都是此式。

$\vert-1\vert=-1$ 是否成立

如果认为 $\vert-1\vert$ 是绝对值，不成立。

如果认为 $\vert-1\vert$ 是一个一阶行列式，成立。然而实际上，一阶行列式用的比较少，且大多数直接写。

例题

计算：

\[D= \begin{vmatrix} 0&1&2&-1\\ -1&0&1&2\\ 0&0&3&-2\\ 0&3&1&-1 \end{vmatrix}\]

答案解析

显然，不选择 $0$ 的排列只有：$\langle-1,1,3,-1\rangle,\langle-1,1,1,-2\rangle,\langle-1,3,2,-2\rangle,\langle-1,3,3,-1\rangle$。

则答案为：$D=-3+2-212+9=-4$。

---

已知：

\[f(x)= \begin{vmatrix} x&1&1&2\\ 1&x&1&-1\\ 3&2&x&1\\ 1&1&2x&1 \end{vmatrix}\]

求 $x^3$ 项的系数。

答案解析

可以发现，可以出现 $x^3$ 项的排列只有两种：$\langle1,2,3,4\rangle,\langle1,2,4,3\rangle$。计算即可，系数为 $1-2=-1$。

转置定理

记方阵 $A$ 的转置方阵为 \(A'\)（也记作 $A^\tau$）。实际上，让 $A$ 关于其主对角线对称即可得到 $A’$。

定义式是从 $n^2$ 个元素中选出不同行且不同列的 $n$ 个元素，然而实际上也有另一种形式：

\[\begin{aligned} D&= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\\ &=\sum_{\langle p_1,p_2,\cdots,p_n\rangle}(-1)^{\tau(p_1,p_2,\cdots,p_n)}a_{1,p_1}a_{2,p_2}a_{3,p_3}\cdots a_{n,p_n}\\ &=\sum_{\langle p_1,p_2,\cdots,p_n\rangle}(-1)^{\tau(p_1,p_2,\cdots,p_n)}a_{p_1,1}a_{p_2,2}a_{p_3,3}\cdots a_{p_n,n}\\ \end{aligned}\]

在定义式中，$p_i$ 对应的是列标，然而现在 $p_i$ 是行标。

显然，这并不影响选出来的元素的组合，因此行列式的值 $D$ 不变。

如果设 \(a'_{i,j}=a_{j,i}\)，则：

\[\sum_{\langle p_1,p_2,\cdots,p_n\rangle}(-1)^{\tau(p_1,p_2,\cdots,p_n)}\prod_{i=1}^na_{p_i,i}=\sum_{\langle p_1,p_2,\cdots,p_n\rangle}(-1)^{\tau(p_1,p_2,\cdots,p_n)}\prod_{i=1}^na'_{p_i,i}\]

而 \(a'_{i,j}\) 即 $a_{i,j}$ 的转置矩阵。

故，行列式的转置的值与其本身的值相等。

即： \(\det A=\det A'\) 这也说明，行列式的“行”与“列”没有什么区别，因此所有关于行列式的“行”的性质均在“列”上适用，下文只介绍“行”，“列”同理可得。

特殊行列式

分别计算以下四个行列式：

行列式中的“留空”

在行列式中，留空不写即为 $0$。

例如下文的 $D_1$ 即：

$$ \begin{vmatrix} a_{1,1}&0&\cdots&0\\ 0&a_{2,2}&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&a_{n,n}\\ \end{vmatrix} $$

\[\begin{aligned} &D_1= \begin{vmatrix} a_{1,1}\\ &a_{2,2}\\ &&\ddots\\ &&&a_{n,n}\\ \end{vmatrix}& D_2= \begin{vmatrix} &&&a_{1,n}\\ &&\dots\\ &a_{n-1,2}\\ a_{n,1} \end{vmatrix} \\ &D_3= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ &a_{2,2}&\cdots&a_{2,n}\\ &&\cdots&\vdots\\ &&&a_{n,n}\\ \end{vmatrix} &D_4= \begin{vmatrix} a_{1,1}\\ a_{2,1}&a_{2,2}\\ \vdots&a_{3,2}&\ddots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\\ \end{aligned}\]

对于 $D_1,D_2$，显然选取 $n$ 个元素，只能是对角线上元素，为：

\[\begin{aligned} D_1&=(-1)^{\tau(1,2,\cdots,n)}a_{1,1}a_{2,2}\cdots a_{n,n}=a_{1,1}a_{2,2}\cdots a_{n,n}\\ D_2&=(-1)^{\tau(n,n-1,\cdots,1)}a_{1,n}a_{2,n-1}\cdots a_{n,1}=(-1)^{\frac{n(n-1)}2}a_{1,n}a_{2,n-1}\cdots a_{n,1}\\ \end{aligned}\]

对于 $D_3,D_4$，在选取第 $i$ 行的元素时，为了这个元素有值，只能选取 $a_{i,i}$，因此同 $D_1,D_2$，有：

\[\begin{aligned} D_3&=(-1)^{\tau(1,2,\cdots,n)}a_{1,1}a_{2,2}\cdots a_{n,n}=a_{1,1}a_{2,2}\cdots a_{n,n}\\ D_4&=(-1)^{\tau(n,n-1,\cdots,1)}a_{1,n}a_{2,n-1}\cdots a_{n,1}=(-1)^{\frac{n(n-1)}2}a_{1,n}a_{2,n-1}\cdots a_{n,1}\\ \end{aligned}\]

我们称形如 $D_1,D_2$ 的行列式为对角行列式，称形如 $D_3$ 的行列式为上三角行列式，称形如 $D_4$ 的行列式为下三角行列式。

一般地，我们计算行列式时，都不是利用定义式计算，而是将其转化为上三角行列式计算。当然，在后文就会发现，其实这四种随便转化一个都能计算。

行列式的展开与递归定义

$n$ 阶行列式可以递归地定义为 $n$ 个 $n-1$ 阶行列式与其系数乘积之和，这有利于研究行列式的性质。

本文中，行列式的性质与行列式的递归定义是相辅相成的。

三阶行列式

可以观察到：

\[\small \begin{aligned} \begin{vmatrix} a_{1,1}&a_{1,2}&a_{1,3}\\ a_{2,1}&a_{2,2}&a_{2,3}\\ a_{3,1}&a_{3,2}&a_{3,3} \end{vmatrix} &=a_{1,1}a_{2,2}a_{3,3}+a_{1,2}a_{2,3}a_{3,1}+a_{1,3}a_{2,1}a_{3,2}-a_{3,1}a_{2,2}a_{1,3}-a_{2,1}a_{1,2}a_{3,3}-a_{1,1}a_{3,2}a_{2,3}\\ &=a_{1,1}(a_{2,2}a_{3,3}-a_{2,3}a_{3,2})-a_{1,2}(a_{2,1}a_{3,3}-a_{2,3}a_{3,1})+a_{1,3}(a_{2,1}a_{3,2}-a_{2,2}a_{3,1})\\ &=a_{1,1} \begin{vmatrix} a_{2,2}&a_{2,3}\\ a_{3,2}&a_{3,3}\\ \end{vmatrix} -a_{1,2} \begin{vmatrix} a_{2,1}&a_{2,3}\\ a_{3,1}&a_{3,3}\\ \end{vmatrix} +a_{1,3} \begin{vmatrix} a_{2,1}&a_{2,2}\\ a_{3,1}&a_{3,2}\\ \end{vmatrix} \end{aligned}\]

可以发现，我们将这个三阶行列式按第一行“展开”了，变成了 $3$ 项，每一项（不考虑正负号）形如：

\[a_{1,j}M_{1,j}\]

我们称行列式中去除第 $i$ 行和第 $j$ 行得到的新 $n-1$ 阶行列式为 $a_{i,j}$ 的余子式，记作 $M_{i,j}$。

记 $(-1)^{i+j}M_{i,j}=A_{i,j}$ 为 $a_{i,j}$ 的代数余子式，则展开后每一项均为 $a_{i,j}A_{i,j}$。

按第一行展开

已知 $n$ 阶行列式：

\[D= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\\\]

在定义式中，在第 $1$ 行选取 $a_{1,j}$，因此得出：

\[\begin{aligned} D&=\sum_{\langle j,p_2,p_3,\cdots,p_n\rangle}(-1)^{\tau(j,p_2,p_3,\cdots,p_n)}a_{1,j}a_{2,p_2}a_{3,p_3}\cdots a_{n,p_n}\\ &=\sum_{j=1}^na_{1,j}\sum_{\langle j,p_2,p_3,\cdots,p_n\rangle}(-1)^{\tau(j,p_2,p_3,\cdots,p_n)}a_{2,p_2}a_{3,p_3}\cdots a_{n,p_n}\\ \end{aligned}\]

显然，$\tau(j,p_2,p_3,\cdots,p_n)=\tau(p_2,p_3,\cdots,p_n)+(j-1)$，因为 $p_2\sim p_n$ 是一个除 $j$ 之外的 $1\sim n$ 的排列，和 $j$ 构成逆序对的数有 $j-1$ 个。因此：

\[\begin{aligned} D&=\sum_{j=1}^na_{1,j}(-1)^{j-1}\sum_{\langle p_2,p_3,\cdots,p_n\rangle}(-1)^{\tau(p_2,p_3,\cdots,p_n)}a_{2,p_2}a_{3,p_3}\cdots a_{n,p_n}\\ &=\sum_{j=1}^na_{1,j}(-1)^{j-1}M_{i,j}\\ &=\sum_{j=1}^na_{1,j}(-1)^{1+j}M_{i,j}\\ &=\sum_{j=1}^na_{1,j}A_{1,j} \end{aligned}\]

这样，我们就将一个 $n$ 阶行列式 $D$ 转化为了 $n$ 个 $n-1$ 阶行列式之和，这是一种递归定义行列式的方法。

同时，也可以发现，$A_{1,j}$ 的正负号是一正一负交替的。

按任意行展开

阅读此部分前，请先阅读“行列式的性质之行交换”。

设有 $n$ 阶行列式 \(\begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i,1}&a_{i,2}&\cdots&a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\)，需要按第 $i$ 行展开。

则可以交换 $i-1$ 次，将第 $i$ 行交换到第 $1$ 行，行列式变为：

\[D=(-1)^{i-1} \begin{vmatrix} a_{i,1}&a_{i,2}&\cdots&a_{i,n}\\ a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\\\]

将第 $i$ 行交换到第 $1$ 行显然不影响 $M_{i,j}$，所以此时可以将行列式按照新的第 $1$ 行（原第 $i$ 行）展开得到：

\[\begin{aligned} D&=(-1)^{i-1}\sum_{j=1}^na_{i,j}(-1)^{1+j}M_{i,j}\\\\ &=\sum_{j=1}^na_{i,j}(-1)^{i+j}M_{i,j}\\ &=\sum_{j=1}^na_{i,j}A_{i,j} \end{aligned}\]

故，行列式可以按照任意行展开。

列展开

由转置定理，可以与行展开类似地展开。

将行列式按第 $j$ 列展开得到：

\[\begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix} =\sum_{i=1}^na_{i,j}A_{i,j}\]

行展开的推论

阅读此部分前，请先阅读“行列式的性质之两行相同值为零”。

设有 $n$ 阶行列式：

\[D= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i,1}&a_{i,2}&\cdots&a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i',1}&a_{i',2}&\cdots&a_{i',n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\]

对于 \(i\neq i'\)，有：

\[\sum_{j=1}^na_{i,j}A_{i',j}=0\]

即：行列式任意行的元素与另一行的对应元素的代数余子式乘积之和为 $0$。

首先，可以构造一个新的行列式 \(D'= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i,1}&a_{i,2}&\cdots&a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i,1}&a_{i,2}&\cdots&a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\)，使得 \(D'\) 中的第 \(i'\) 行是 $D$ 的第 $i$ 行，其余行与 $D$ 一致。

又因为 \(D'\) 中第 $i$ 行与第 \(i'\) 行相同，因此 \(D'=0\)。

将行列式 \(D'\) 按照第 \(i'\) 行展开，得到：

\[0= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i,1}&a_{i,2}&\cdots&a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i,1}&a_{i,2}&\cdots&a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}=\sum_{j=1}^na_{i,j}A_{i',j}\]

即：

\[\sum_{j=1}^na_{i,j}A_{i',j}=0\]

行列式的性质

设 $n$ 阶行列式：

\[D= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\\\]

由转置定理，行列式的性质在“列”上仍然适用。

行交换

交换行列式第 \(i,i'\) 行（\(i\neq i'\)），行列式的值会乘上 $-1$。

即：

\[D= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i,1}&a_{i,2}&\cdots&a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i',1}&a_{i',2}&\cdots&a_{i',n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix} =- \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i',1}&a_{i',2}&\cdots&a_{i',n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i,1}&a_{i,2}&\cdots&a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\]

以交换 $1,2$ 行为例。

在定义式中，设第 $1$ 行选择了 $a_{1,p_1}$，第 $2$ 行选择了 $a_{2,p_2}$。

交换之后，设新方阵为 \(a'\)，不妨令选择元素不变，则选择了 \(a'_{1,p_2},a'_{2,p_1}\)。

在定义式中，即交换了排列中的 $p_1,p_2$，这会使 $\tau(p_1,p_2,p_3,\cdots,p_n)$ 发生 $1$ 的变化，则 $(p_1,p_2)$ 对行列式的贡献会乘上 $-1$。

所以，整个行列式的值会乘上 $-1$。

推广到任意两行也是一样的。

两行相同值为零

若行列式 $D$ 存在两行相同，则 $D=0$。

因为我们可以交换这两行，得到 $D=-D$，即 $D=0$。

在方程组中，即无数解。

行倍乘

将行列式第 $i$ 行乘上一个数 $k$，行列式也会乘 $k$。

即：

\[k\cdot D= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ k\cdot a_{i,1}&k\cdot a_{i,2}&\cdots&k\cdot a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\\\]

将行列式按照第 $i$ 行展开，得到：

\[\begin{aligned} D&= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i,1}&a_{i,2}&\cdots&a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix} \\ &=\sum_{j=1}^na_{i,j}A_{i,j} \end{aligned}\]

将第 $i$ 行全部乘上 $k$，得到：

\[\sum_{j=1}^n(k\cdot a_{i,j})A_{i,j}=k\sum_{j=1}^na_{i,j}A_{i,j}\]

显然，第 $i$ 行乘 $k$ 并不影响 $A_{i,j}$，所以行列式的值变为了原来的 $k$ 倍。

两行成比值为零

将其中一行除以比例 $k$，得到这两行相同，$D=\dfrac0k=0$。

在方程组中，即无数解。

行倍乘的推论

行列式中行内公因子可以提取到行列式外，即：

\[\begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ k\cdot a_{i,1}&k\cdot a_{i,2}&\cdots&k\cdot a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix} = k\begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i,1}&a_{i,2}&\cdots&a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\\\]

行倍加

将行列式第 $i$ 行乘上一个数 $k$，加到第 $i’$ 行上（\(i\neq i'\)，且第 $i$ 行不变），行列式值不变。

即：

\[D= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i,1}&a_{i,2}&\cdots&a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i',1}&a_{i',2}&\cdots&a_{i',n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix} = \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i,1}&a_{i,2}&\cdots&a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i',1}+k\cdot a_{i,1}&a_{i',2}+k\cdot a_{i,2}&\cdots&a_{i',n}+k\cdot a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\]

令行列式 \(D'=\begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i,1}&a_{i,2}&\cdots&a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{i',1}+k\cdot a_{i,1}&a_{i',2}+k\cdot a_{i,2}&\cdots&a_{i',n}+k\cdot a_{i,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\)。

由行展开的推论，将 \(D'\) 按照第 \(i'\) 行展开，得到：

\[\begin{aligned} D'&=\sum_{j=1}^n(a_{i',j}+k\cdot a_{i,j})A_{i',j}\\ &=\sum_{j=1}^na_{i',j}A_{i',j}+k\sum_{j=1}^na_{i,j}A_{i',j}\\ &=D+0k\\ &=D \end{aligned}\]

故，将行列式第 $i$ 行乘上一个数 $k$，加到第 \(i'\) 行上（\(i\neq i'\)，且第 $i$ 行不变），行列式值不变。

行列式求解

定义式法

枚举排列计算即可，时间复杂度 $\mathcal O(n!)$。

递归法

枚举按照行或列展开计算，时间复杂度 $\mathcal O\left(n^2n!\right)$。

高斯消元法

与高斯消元类似的方法。

可以通过行交换和行倍加来“消元”，将原本的行列式转化为“上三角行列式”计算。

例如，计算：

\[D= \begin{vmatrix} 1&2&3\\ 4&5&6\\ 7&8&9\\ \end{vmatrix}\]

将第 $1$ 行乘 $-4$ 加到第 $2$ 行，乘 $-7$ 加到第 $3$ 行得到：

\[D= \begin{vmatrix} 1&2&3\\ &-3&-6\\ &-6&-12 \end{vmatrix}\]

将第 $2$ 行乘 $-2$ 加到第 $3$ 行得到：

\[\begin{aligned} D&= \begin{vmatrix} 1&2&3\\ &-3&-6\\ &&0 \end{vmatrix}\\ &=1\times(-3)\times0\\ &=0 \end{aligned}\]

---

好似很顺利，但是如果在 $a_{i,i}$ 出现了 $0$ 而 $i\neq n$ 怎么办呢？

可以直接在第 $i+1\sim n$ 行中找第 $k$ 行满足 $a_{k,i}\neq0$，然后交换第 $i$ 行和第 $k$ 行，继续计算，注意不要忘记乘上 $-1$。

如果找不到满足 $a_{k,i}\neq0$ 的 $k$，即行列式值为 $0$（最终上三角行列式中主对角线上一定有 $0$）。

可以借助方程组理解：将行列式视为方程组的系数方阵，有一个未知数的系数为 $0$，要么无解，要么无数解；而无论哪种情况，行列式的值都为 $0$。

例题

计算：

\[D=\begin{vmatrix} a^2&ab&b^2\\ 2a&a+b&2b\\ 1&1&1 \end{vmatrix}\]

答案解析

首先为了方便计算，进行两次行交换得到：

$$ D=\begin{vmatrix} 1&1&1\\ a^2&ab&b^2\\ 2a&a+b&2b \end{vmatrix} $$

随后进行行倍加：

$$ \begin{aligned} D&=\begin{vmatrix} 1&1&1\\ a^2&ab&b^2\\ 2a&a+b&2b \end{vmatrix}\\ &=\begin{vmatrix} 1&1&1\\ &a(b-a)&(b+a)(b-a)\\ &b-a&2(b-a)\\ \end{vmatrix}\\ &=\begin{vmatrix} 1&1&1\\ &a(b-a)&(b+a)(b-a)\\ &&2(b-a)-\dfrac{(b+a)(b-a)}{a}\\ \end{vmatrix}\\ &=1\cdot a(b-a)\left[2(b-a)-\dfrac{(b+a)(b-a)}{a}\right]\\ &=(a-b)^3 \end{aligned} $$

---

计算 $n$ 阶行列式：

\[D=\begin{vmatrix} a&&&&1\\ &a\\ &&a\\ &&&\ddots\\ 1&&&&a \end{vmatrix}\]

答案解析

将第一行乘 $-\dfrac1a$ 后加到最后一行，可得：

$$ \begin{aligned} D&=\begin{vmatrix} a&&&&1\\ &a\\ &&a\\ &&&\ddots\\ 0&&&&a-\dfrac1a \end{vmatrix}\\ &=a^{n-1}\left(a-\dfrac1a\right)\\ &=a^n-a^{n-2} \end{aligned} $$

克拉默法则

也译作“克拉姆法则”。

设有 $n$ 元线性方程组：

\[\begin{cases} a_{1,1}x_1+a_{1,2}x_2+\cdots+a_{1,n}x_n=b_1\\ a_{1,1}x_1+a_{1,2}x_2+\cdots+a_{1,n}x_n=b_2\\ \cdots\\ a_{n,1}x_1+a_{n,2}x_2+\cdots+a_{n,n}x_n=b_n\\ \end{cases}\]

设 $D_0$ 为其系数方阵行列式：

\[D_0= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\ \end{vmatrix}\\\]

当 $D_0\neq0$ 时，方程组有定解，假设 $D_0\neq0$，则方程组的解为：

\[\begin{cases} x_1=\dfrac{D_1}{D_0}\\ x_2=\dfrac{D_2}{D_0}\\ x_3=\dfrac{D_3}{D_0}\\ \cdots\\ x_n=\dfrac{D_n}{D_0}\\ \end{cases}\]

其中，$D_j(1\leq j\leq n)$ 是把 $D_0$ 的第 $j$ 列替换为 \(\begin{pmatrix}b_1\\b_2\\\vdots\\b_n\end{pmatrix}\) 得到的 $n$ 阶行列式，即：

\[D_j= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,j-1}&b_1&a_{1,j+1}&a_{1,j+2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,j-1}&b_2&a_{2,j+1}&a_{2,j+2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,j-1}&b_n&a_{n,j+1}&a_{n,j+2}&\cdots&a_{n,n}\\ \end{vmatrix}\]

但是你用消元法解方程不是更快吗？克拉默法则多用于理论推导。

---

例如对于线性方程组： \(\begin{cases} x_1+x_2=3\\ 2x_1+3x_2=8 \end{cases}\)

有：

\[\begin{aligned} D_0&=\begin{vmatrix} 1&1\\ 2&3 \end{vmatrix}=1\\ D_1&=\begin{vmatrix} 3&1\\ 8&3 \end{vmatrix}=1\\ D_2&=\begin{vmatrix} 1&3\\ 2&8 \end{vmatrix}=2 \end{aligned}\]

所以，方程组得解为：

\[\begin{cases} x_1=\dfrac{D_1}{D_0}=1\\ x_2=\dfrac{D_2}{D_0}=2\\ \end{cases}\]

---

证明

设 $n$ 元线性方程组为：

\[\begin{cases} a_{1,1}x_1+a_{1,2}x_2+\cdots+a_{1,n}x_n=b_1\\ a_{1,1}x_1+a_{1,2}x_2+\cdots+a_{1,n}x_n=b_2\\ \cdots\\ a_{n,1}x_1+a_{n,2}x_2+\cdots+a_{n,n}x_n=b_n\\ \end{cases}\]

则有系数方阵为：

\[A= \begin{pmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n} \end{pmatrix}\]

其行列式为：

\[D_0=\det A= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,n} \end{vmatrix}\]

根据 $D_j$ 的定义，有：

\[D_j= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,j-1}&b_1&a_{1,j+1}&a_{1,j+2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,j-1}&b_2&a_{2,j+1}&a_{2,j+2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,j-1}&b_n&a_{n,j+1}&a_{n,j+2}&\cdots&a_{n,n}\\ \end{vmatrix}\]

考虑到 $b_i=\sum\limits_{j=1}^na_{i,j}x_j$，有：

\[D_j= \begin{vmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,j-1}&\sum\limits_{k=1}^na_{1,k}x_k&a_{1,j+1}&a_{1,j+2}&\cdots&a_{1,n}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,j-1}&\sum\limits_{k=1}^na_{2,k}x_k&a_{2,j+1}&a_{2,j+2}&\cdots&a_{2,n}\\ \vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\ a_{n,1}&a_{n,2}&\cdots&a_{n,j-1}&\sum\limits_{k=1}^na_{n,k}x_k&a_{n,j+1}&a_{n,j+2}&\cdots&a_{n,n}\\ \end{vmatrix}\]

将 $D_j$ 按照第 $j$ 列展开，得到：

\[\begin{aligned} D_j&=\sum_{i=1}^na_{i,j}A_{i,j}\\ &=\sum_{i=1}^n\left(\sum_{k=1}^na_{i,k}x_k\right)A_{i,j}\\ &=\sum_{k=1}^nx_k\sum_{i=1}^na_{i,k}A_{i,j} \end{aligned}\]

• 当 $k=j$ 时，有：

  \[x_j\sum_{i=1}^na_{i,j}A_{i,j}=x_j\cdot D_0\]

  即：将 $D_j$ 以第 $j$ 列展开，得到 $\sum\limits_{i=1}^na_{i,j}A_{i,j}=D_0$。

• 当 $k\neq j$ 时，有：

  \[x_k\sum_{i=1}^na_{i,k}A_{i,j}=x_k\cdot0=0\]

  由行展开的推论可得，$\sum\limits_{i=1}^na_{i,k}A_{i,j}=0$。

故，$D_j=x_j\cdot D_0+0=x_j\cdot D_0$。

故，$\dfrac{D_j}{D_0}=\dfrac{x_j\cdot D_0}{D_0}=x_j$。

即，原线性方程组的解为：

\[\begin{cases} x_1=\dfrac{D_1}{D_0}\\ x_2=\dfrac{D_2}{D_0}\\ x_3=\dfrac{D_3}{D_0}\\ \cdots\\ x_n=\dfrac{D_n}{D_0}\\ \end{cases}\]

齐次线性方程组与非齐次线性方程组

即常数项均为 $0$ 的线性方程组，例如 \(\begin{cases}2x+3y=0\\x+y=0\end{cases}\) 就是齐次线性方程组，而 \(\begin{cases}2x+3y=1\\x+y=0\end{cases}\) 就是一个非齐次线性方程组。

对于齐次线性方程组，显然存在一组解：$x_1=x_2=x_3=\cdots=x_n=0$，称为“零解”。

而研究的重点显然是是否存在“非零解”。如果存在，则有无数解。

代码例题：行列式求值

很容易写出代码（时间复杂度为 $\mathcal O\left(n^3\right)$）：

然而交上去一看，发现只有 $58\text{pts}$，为什么呢？注意到模数 $p$ 可能不为质数，无法使用乘法逆元。

辗转相减法

我们需要另一种方法来消元——辗转相减法，这样可以避免除法。

但是注意，辗转相减后交换的时候行列式的值会变为原来的 $-1$ 倍。

时间复杂度：$\mathcal O(n^3\log V)$，其中 $\mathcal O(\log V)$ 是辗转相减法带来的，$V$ 为 $a$ 的值域大小，在本题中 $V=10^9+7$。

---

• Previous
  [NOIP 2017 提高组] 列队
• Next
  题解：[NOI2012] 随机数生成器

---