洛谷自建题目链接

数据包

题目

题目描述

GKK 是一个喜欢环上游戏的男孩。

现在有一张 $n$ 个点组成的图，每个点的编号为 $0\sim n-1$。你有 $m$ 次操作，每一次操作有三个参数 $a,b,c$。操作的意义如下：

在编号为 $a+0,b+0$ 的点之间连一条边权为 $c+0$ 的边。
在编号为 $b+0,a+1$ 的点之间连一条边权为 $c+1$ 的边。
在编号为 $a+1,b+1$ 的点之间连一条边权为 $c+2$ 的边。
在编号为 $b+1,a+2$ 的点之间连一条边权为 $c+3$ 的边。
在编号为 $a+2,b+2$ 的点之间连一条边权为 $c+4$ 的边。
在编号为 $b+2,a+3$ 的点之间连一条边权为 $c+5$ 的边。
……

其中，点的编号都是模 $n$ 意义下的，即 $n$ 号点与 $0$ 号点等价，$2n-1$ 号点与 $n-1$ 号点等价。

为了方便理解，下图为 $n=16,a=17,b=14,c=7$ 时首先加入的 $7$ 条边。

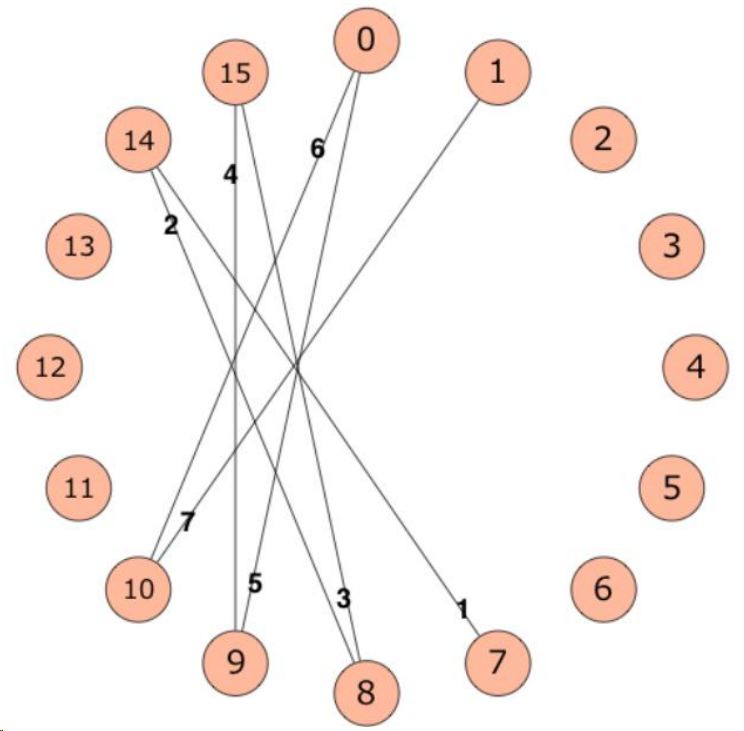
GKK 想知道，在所有操作进行完毕之后，图的最小生成树的各边权值之和。他把这个问题抛给了你。

最小生成树的定义：从 $n$ 个点的图中选出 $n-1$ 条边，使图联通且所选边的权值和最小。

输入格式

第一行两个正整数 $n,m$ 表示点数和操作数。

接下来 $m$ 行，每行三个非负整数 $a,b,c$ 表示一次操作。

输出格式

一行一个整数表示答案。

输入输出样例

输入样例 #1

7 1
5 2 1

输出样例 #1

21

输入样例 #2

2 1
0 0 1000000000

输出样例 #2

1000000001

输入样例 #3

输出样例 #3

42

说明/提示

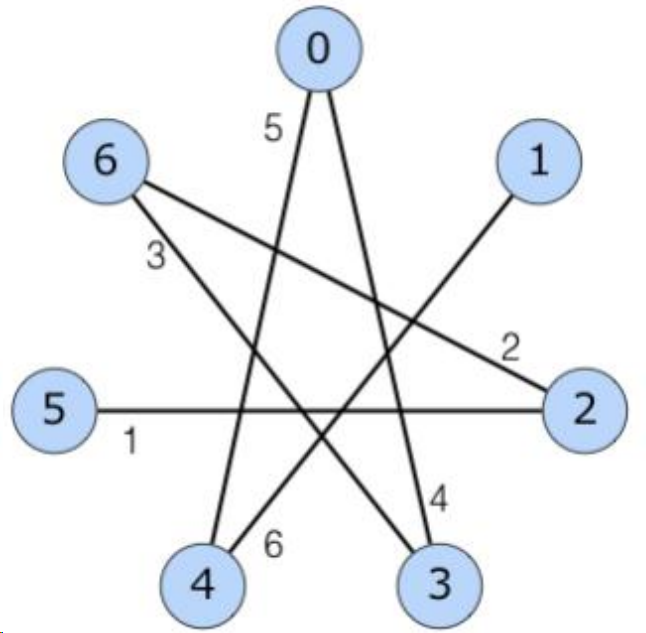
样例解释 #1

最小生成树如图，答案为 $1+2+3+4+5+6=21$。

数据范围

对于 $100\%$ 的数据，满足 $2\leq n\leq 2\times 10^5,1\leq m\leq2\times10^5$。

提示

可能存在重边或自环。
边权也许可以构成一个等差数列，公差为 $2$。

题解

题意分析

求最小生成树，考虑 Kruskal 算法。

但是边的数量会达到 $\mathcal O\left(n^2\right)$ 的量级，直接 Kruskal 会 $\text{TLE}$。

对于每一次操作，其会连边：

\[\begin{aligned} (a,b)&=c+0\\ (a+1,b+1)&=c+2\\ (a+2,b+2)&=c+4\\ &\cdots \end{aligned}\]

以及：

\[\begin{aligned} (a+1,b)&=c+1\\ (a+2,b+1)&=c+3\\ (a+3,b+2)&=c+5\\ &\cdots \end{aligned}\]

因此我们可以仅在操作时连边 $(a,b),(a+1,b)$，然后在 Kruskal 的过程中一边操作一边连边。

对于边 $(u,v)=w$，其下一条边就是 $(u+1,v+1)=w+2$。

这样做并不会影响正确性，因为边 $(u+1,v+1)=w+2$ 在原本的 Kruskal 算法中本来就是后于 $(u,v)=w$ 查询的。

而也仅仅当边 $(u,v)=w$ 被加入最小生成树中时，我们需要连 $(u+1,v+1)=w+2$。

如何证明 $(u,v)=w$ 不在生成树中时，$(u+1,v+1)=w+2$ 不需要连呢？

考虑 Kruskal 算法求最小生成树的过程，此时即 $u,v$ 已经在一个连通块中，则 $u,v$ 已经连通。

一定存在边 $(u+1,v)=w+1$，较 $(u+1,v+1)$ 更优。

AC 代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
typedef long long ll;
constexpr const int N=2e5,M=2e5;
int n;
struct edge{
	int u,v;
	ll w;
};
bool operator >(edge a,edge b){
	return a.w>b.w;
}
priority_queue<edge,vector<edge>,greater<edge>>q;
int f[N+1];
int find(int x){
	if(f[x]!=x){
		return f[x]=find(f[x]);
	}
	return x;
}
void merge(int x,int y){
	f[find(x)]=find(y);
}
ll Kruskal(){
	for(int i=1;i<=n;i++){
		f[i]=i;
	}
	ll ans=0;
	while(q.size()){
		auto p=q.top();q.pop();
		if(find(p.u)!=find(p.v)){
			ans+=p.w;
			merge(p.u,p.v);
			q.push({(p.u+1)%n,(p.v+1)%n,p.w+2});
		}
	}
	return ans;
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	int m;
	cin>>n>>m;
	while(m--){
		int a,b;
		ll c;
		cin>>a>>b>>c;
		a%=n;b%=n;
		q.push({a,b,c});
		q.push({(a+1)%n,b,c+1});
	}
	cout<<Kruskal()<<'\n';
	
	cout.flush();
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

题解：GKK 的游戏

题目见正文 | 最小生成树

题目