为什么这么近就重题了。
题意分析
如果不考虑合并 $k$ 次的限制,就是一个普通的合并石子问题,思路即将小堆合并到大堆上,这样小堆的计算次数会更多,大堆的计算次数会更少,进而使得总代价最小。
考虑加入 $k$ 次限制之后总代价的形式:
- 存在 $1$ 个 $a_i$ 满足 $a_i$ 不在总代价中。
- 存在 $k$ 个 $a_i$ 满足 $a_i$ 被计算了 $1$ 次。
- 存在 $k^2$ 个 $a_i$ 满足 $a_i$ 被计算了 $2$ 次。
- ……
- 存在 $n$ 个 $a_i$ 满足 $a_i$ 被计算了 $\left\lceil\log_k n\right\rceil$ 次。
具体可以参考此图:
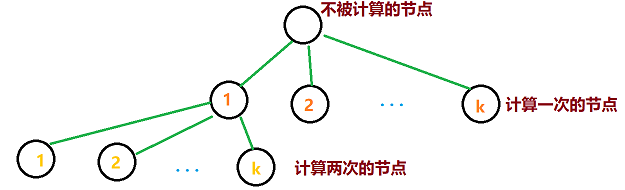
我们可以以 $a_i$ 为节点建一棵树(代码中不需要,仅仅为了便于分析),那么一个节点与父节点的连边代表合并到父节点上。
则可以解释上文的结论,根节点的 $x$ 级子节点有 $k^x$ 个,而这些子节点的答案被统计了 $x$ 次(合并一次就会被统计一次)。
则一个节点对总代价的贡献为其值乘深度,这也是建树的做法。
然而,我们可以考虑令较大的 $a_i$ 被统计的次数尽可能少,直接排序后贪心统计即可。
同时又考虑到 $k$ 可能相同,可以预处理出 $k=1,2,3,\cdots,n$ 的情况的答案 $ans_k$,询问时直接输出即可。注意当 $k>n$ 时,答案同 $k=n$ 的情况。
时间复杂度:$\mathcal O(n\log n)$。
AC 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
//#define int long long
typedef long long ll;
constexpr const int N=1e5;
int n,a[N+1];
ll sum[N+1],ans[N+1];
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",a+i);
}
sort(a+1,a+n+1);
for(int i=1;i<=n;i++){
sum[i]=sum[i-1]+a[i];
}
for(int k=1;k<=n;k++){
//p=n-1:a[n]不统计
int p=n-1,pl=1;
ll kk=k;//kk=k^pl
while(p>=kk){
ans[k]+=(sum[p]-sum[p-kk])*pl;//这一层的kk个元素统计答案
p-=kk;kk*=k;
pl++;
}
ans[k]+=sum[p]*pl;
}
int q;
scanf("%d",&q);
while(q--){
int k;
scanf("%d",&k);
k=min(k,n);
printf("%lld ",ans[k]);
}putchar(10);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}