割点
所谓割点,就是连通图中的某一个点满足删除该点后,原图不再连通。
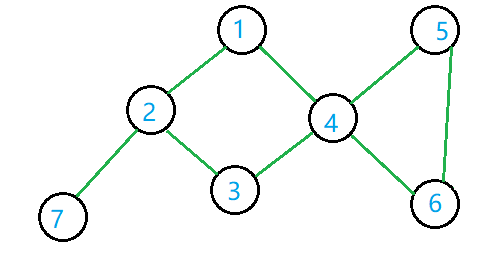
如图中的 $2,4$ 就是一个割点。
但需要注意的是,割点不一定在环上,比如:

图中的 $2$ 就是割点。
不过存在特殊情况:

该图没有割点,无论去掉 $1$ 还是 $2$,最后都会剩下一个节点。
关于“割点”不同的定义
如同平衡树中的“左旋”与“右旋”,割点的定义也有不同的说法。(上文是主流说法)
比如说第三张图中只有两个节点,有人认为这两个都是割点,即剩下的那个节点不连通。
无向图 Tarjan 求割点
前置知识:Tarjan 求强连通分量
无向图 Tarjan 求割点
前向边与横边不存在
见此处。
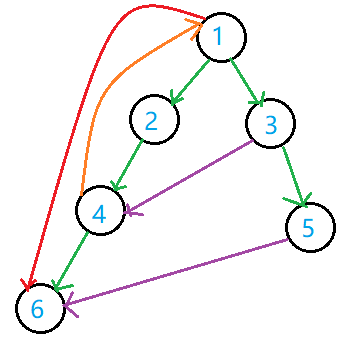
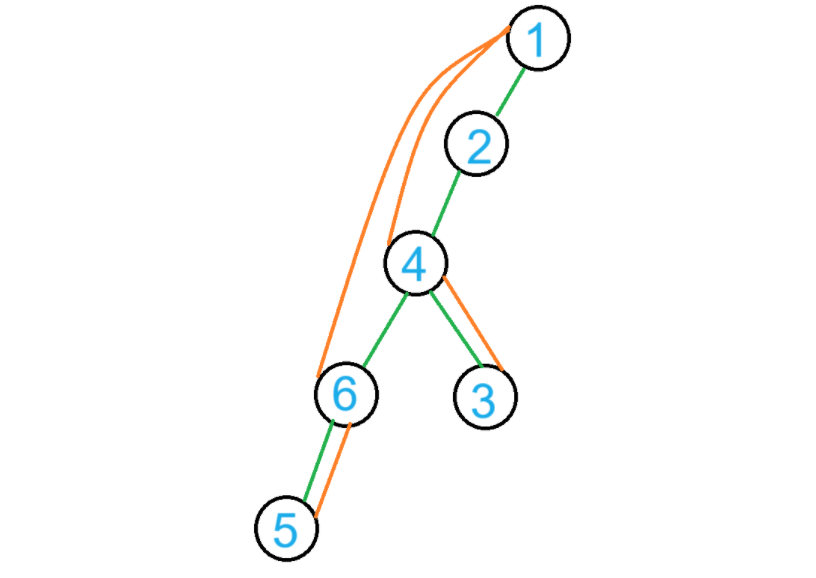
一棵有向图的 DFS 生成树如图:
图中绿色为普通树边,橙色为回溯边,红色为前向边,紫色为横边。
考虑到无向图,实际上 DFS 生成树中只有普通树边和回溯边。
前向边不存在,因为无向,因此前向边反向就是一条回溯边。
横边不存在,因为按照 DFS 搜索顺序不会使其有可能存在。
例如图中搜索到 $4$ 之后,按照 DFS 的原则会先后搜索 $3,6$,不可能只搜索 $6$ 然后回退至 $1$ 再搜索到 $3$,然后连横边。
即化为:
一定不为割点的情况
当该节点是 DFS 生成树的叶节点或只有一个子节点的根节点。
- 叶节点显然不影响生成树的连通。
- 根节点如果只有一个子节点,那么该子节点可以成为新的根节点,不影响连通。
割点的判定
令节点 $x$ 的子节点为节点 $y_1,y_2,y_3,\cdots,y_k$,则删除节点 $x$ 后其所在连通块会分裂为 $k+1$ 个部分:$y_1,y_2,y_3,\cdots,y_k$ 和父节点及其子树。
那么我们需要判断的就是能否使其分裂为至少 $2$ 个部分。
当节点 $x$ 为根节点时,需要分裂出至少两个符合以下规定的部分。
因为父节点的部分肯定是能够分裂出来的,因此当 $x$ 不为根节点时,需要分裂出至少一个符合以下规定的部分。
由于 DFS 生成树的性质,$dfn_{y_i}$ 肯定是大于 $dfn_x$ 的。
那么 $low_{y_i}$ 初始时为 $dfn_{y_i}$ 也大于 $dfn_x$。
因此若求出来的 $low_{y_i}\geq dfn_x$,则代表其是节点 $x$ 的子节点部分。
但是存在一个问题:如果只需要分裂出一个很好判断,然而当 $x$ 为根节点时需要判断两个,如何判断 $y_i$ 之间有没有连接呢?
不需要判断,$y_i$ 之间绝对没有连接。
由无向图,不存在横边,因此 $y_i$ 之间想要连接只能够通过公共祖先,然而 $x$ 为根节点是其子节点的唯一公共祖先。
因此当 $x$ 为根节点时,$y_i$ 之间不会相连。
子节点数 son 计算代码:
1
if(low[v]>=dfn[x])son++;
答案记录:
1
2
3
4
5
if(x==root){
if(son>1)ans.push_back(x);
}else{
if(son>0)ans.push_back(x);
}
例题 AC 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=5e5,M=2e6;
struct graph{
struct edge{
int v,r;
}a[2*M+1];
int h[N+1];
void create(int u,int v){
static int top=1;
a[++top]={v,h[u]};
h[u]=top;
}
}g;
int dfn[N+1];
vector<int>ans;
void Tarjan(int x,int root){
static int cnt,low[N+1];
dfn[x]=low[x]=++cnt;
int son=0;
for(int i=g.h[x];i;i=g.a[i].r){
int &v=g.a[i].v;
if(!dfn[v]){
Tarjan(v,root);
low[x]=min(low[x],low[v]);
if(low[v]>=dfn[x])son++;
}else low[x]=min(low[x],dfn[v]);
}
if(x==root){
if(son>1)ans.push_back(x);
}else{
if(son>0)ans.push_back(x);
}
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
int n,m;
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++){
int u,v;
scanf("%d %d",&u,&v);
g.create(u,v);
g.create(v,u);
}
for(int i=1;i<=n;i++){
if(!dfn[i])Tarjan(i,i);
}
sort(ans.begin(),ans.end());
printf("%d\n",ans.size());
for(int &i:ans)printf("%d ",i);
putchar(10);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}