例题链接

只有有向图有强连通分量

无向图没有“强连通分量”这个概念，只有“连通块”。

无向图请看边双连通分量和点双连通分量。

引入

例题：

给定一个 $n$ 个点 $m$ 条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

权值大于等于 $0$。

这明显需要考虑环，因为从环上任何一个节点进入环之后，整个环都可以被遍历到，肯定更优，并且能够去到更多的节点。

因此我们可以将所有 强连通分量 都变成一个节点来顶替其原来的位置，并重新建图，使原图成为一个有向无环图后求解。

有向图 Tarjan 求强连通分量

有向图下 DFS 生成树

我们需要先了解一下 DFS 生成树。

如图：

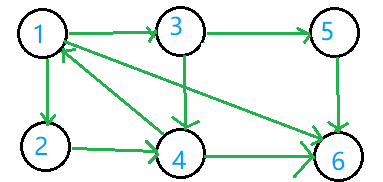
其可能的 DFS 生成树是：

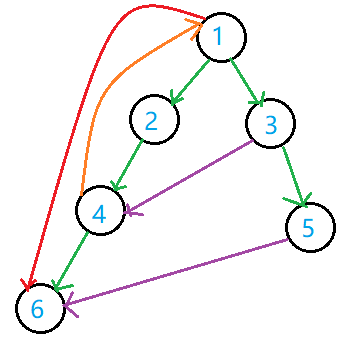
~~显然，这并不是一棵树。~~

边分为四种：

树边（如 $1\sim 2$）：使用绿色标注，指向子节点。
回溯边（如 $4\sim 1$）：使用橙色标注，又称返祖边、回边，指向祖先节点。
前向边（如 $1\sim 6$）：使用红色标注，指向子节点的子树中的某一节点。
横边（如 $3\sim 4$）：使用紫色标注，又称横叉边，指向当前节点某一祖先的另一子树中的节点。

Tarjan 算法流程

维护信息

在深搜的同时，维护 $dfn_i,low_i$、一个栈 $s$ 和一个标记数组 $flag_i$ 用于标记 $i$ 是否位于栈 $s$ 内。

$dfn_x$ 表示 $x$ 的时间戳，即 DFS 序中第几个被搜索到的节点。

$low_x$ 表示 $x$ 在 DFS 生成树中能够回退到的最早的位置，这个位置在求解 $x$ 时需要在栈 $s$ 中。

每当搜索到一个节点 $x$ 时，就将其加入栈 $s$，并标记 $flag_x=1$。注意，栈 $s$ 不是 DFS 搜索栈，不应当在递归结束前出栈。

更新信息

对于 $dfn_x,low_x$，最初的初始值都是其时间戳。

$low_x$ 为其时间戳即表示其至少能够回退至自己。

遍历 $x$ 的子节点 $y$，若 $dfn_y=0$ 则代表还没有搜索过，进行搜索完成之后用 $low_y$ 来更新 $low_x$：

\[low_x=\min(low_x,low_y)\]

因为 $x$ 有可能先走到子节点 $y$，然后再从子节点通过回溯边走到更高（更早）的位置，因此需要更新。

但是若 $dfn_y\neq 0$，则代表已经搜索过，这时需要通过 $flag$ 判断其是否在栈 $s$ 中。

首先，$(x,y)$ 不可能是树边，因为 DFS 生成树显然是按照树边的顺序分配 $dfn$ 的。

如果在栈 $s$ 中，代表 $y$ 已经访问过，是 $x$ 的祖先节点，则边 $(x,y)$ 是一条回溯边，更新答案：
\[low_x=\min(low_x,dfn_y)\]
如果不是，则代表边 $(x,y)$ 是一条前向边或横边，不能够更新答案。

为什么不在栈 $s$ 中就是前向边或横边？

此处不是树边，原因见上文。

因为 $y$ 本来应该是 $x$ 的子节点，按照树边未曾被访问过，但是却已经被其他节点作为父节点访问过了（所以 $dfn_y>0$），而又在栈中，代表 $y$ 其实是 $x$ 的祖先节点。即回溯边。

当通过子节点更新完成之后，如果仍然有 $dfn_x=low_x$，则代表 $x$ 是这个强连通分量在DFS 生成树上的根节点。

因为 $dfn_x=low_x$ 代表 $x$ 的子树中，没有路径能够使 $x$ 走出去~~是条死路~~。

这时，我们再将栈 $s$ 中 $x$ 及在 $x$ 之后加入栈的元素全部出栈，这些元素就是一个强连通分量。

参考代码

//old是原图
int dfn[N+1],id[N+1];
void Tarjan(int x){
	static bool flag[N+1];
	static int top,s[N+1],low[N+1];
	dfn[x]=low[x]=++top;
	s[top]=x;
	flag[x]=true;
	for(int i=old.h[x];i;i=old.a[i].r){
		if(!dfn[old.a[i].v]){
			Tarjan(old.a[i].v);
			low[x]=min(low[x],low[old.a[i].v]);
		}else{
			if(flag[old.a[i].v]){
				low[x]=min(low[x],dfn[old.a[i].v]);
			}
		}
	}
	if(dfn[x]==low[x]){
		build.n++;
		while(s[top]!=x){
            //s[top]即强连通分量中的点
            //...
			top--;
		}//...
		top--;
	}
}

例题 AC 代码

Tarjan 缩点后重新建图成为有向无环图，并且进行拓扑排序后即可 DP 求解。

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=1e4,M=1e5;
struct graph{
	struct edge{
		int v,r;
	}a[M+1];
	
	int n,h[N+1],value[N+1],top;
	void create(int u,int v){
		a[++top]={v,h[u]};
		h[u]=top;
	}
}old,build;
//Tarjan缩点
int dfn[N+1],id[N+1];
void Tarjan(int x){
	static bool flag[N+1];
	static int top,cnt,s[N+1],low[N+1];
	dfn[x]=low[x]=++cnt;
	s[++top]=x;//此处的top其实可以是双重含义(时间戳计数器&栈计数器),由于top--只会发生在递归之后,因此不会出错,但需要注意不要混用,求点双连通分量时混用会出错!!
	flag[x]=true;
	for(int i=old.h[x];i;i=old.a[i].r){
		if(!dfn[old.a[i].v]){
			Tarjan(old.a[i].v);
			low[x]=min(low[x],low[old.a[i].v]);
		}else{
			if(flag[old.a[i].v]){
				low[x]=min(low[x],dfn[old.a[i].v]);
			}
		}
	}
	if(dfn[x]==low[x]){
		build.n++;
		while(s[top]!=x){
			flag[s[top]]=false;
			id[s[top]]=build.n;
			build.value[build.n]+=old.value[s[top]];//建新图,合并节点信息
			top--;
		}flag[s[top]]=false;
		id[s[top]]=build.n;
		build.value[build.n]+=old.value[s[top]];
		top--;
	}
}//重新建图
void Build(){
	for(int i=1;i<=old.n;i++){
		for(int j=old.h[i];j;j=old.a[j].r){
			int &u=id[i],&v=id[old.a[j].v];
			if(u==v)continue;
			build.create(u,v);
		}
	}
}//拓扑排序
int order[N+1]; 
void topSort(){
	static int in[N+1];
	for(int i=1;i<=build.n;i++){
		for(int j=build.h[i];j;j=build.a[j].r){
			in[build.a[j].v]++;
		}
	}
	int front=1,rear=1;
	for(int i=1;i<=build.n;i++){
		if(in[i]==0)order[rear++]=i;
	}
	while(front<rear){
		int u=order[front++];
		for(int i=build.h[u];i;i=build.a[i].r){
			int v=build.a[i].v;
			if(--in[v]==0)order[rear++]=v;
		}
	}
}//DP求解
int Dp(){
	static int dp[N+1];
	for(int i=1;i<=build.n;i++){
		dp[i]=build.value[i];
	}
	for(int i=1;i<=build.n;i++){
		int &u=order[i];
		for(int j=build.h[u];j;j=build.a[j].r){
			int &v=build.a[j].v;
			dp[v]=max(dp[v],dp[u]+build.value[v]);
		}
	}
	int Max=0;
	for(int i=1;i<=build.n;i++){
		Max=max(Max,dp[i]);
	}return Max;
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	int n,m;
	scanf("%d %d",&n,&m);
	old.n=n;
	for(int i=1;i<=n;i++){
		scanf("%d",old.value+i);
	}
	for(int i=1;i<=m;i++){
		int u,v;
		scanf("%d %d",&u,&v);
		old.create(u,v);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]){
			Tarjan(i);
		}
	}
	Build();
	topSort();
	printf("%d\n",Dp());
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

有向图 Tarjan 求强连通分量详解

有向图 Tarjan 缩点 | 例题：洛谷P3387

引入