题目传送门

加强版数据包

加强版数据包满足 $2\leq n\leq 200000$，需要使用 $\mathcal O\left(n\log n\right)$ 做法。

题意分析

给定一棵无根树，最开始花费 $1$ 时刻可以选择一个节点告知一条消息，每一个时刻每一个已知消息的节点都可以告知其他一个节点，求消息传遍整棵树的最短时间和最开始能选择的节点有哪些。

$\mathcal O\left(n^2\log n\right)$ 做法

树形 DP

状态设计

令 $dp_x$ 表示在从节点 $x$ 开始（不包括），告知整个 $x$ 的子树的最少时间。

很明显，当根节点不同时，节点 $x$ 的子树并不确定。

因此我们的 $dp_x$ 不通用。

但是，我们可以枚举根节点 $i$，那样我们选择节点 $i$ 作为第一个接收到消息的节点，每一次都重新递推一遍 $dp_i$，$dp_i$ 即选择节点 $i$ 的答案，最终取最大值即可。

状态转移

如何递推呢？

对于节点 $x$ 和其子节点 $y_1,y_2,y_3,\cdots,y_k$，我们先考虑一下如何传递。

如图：

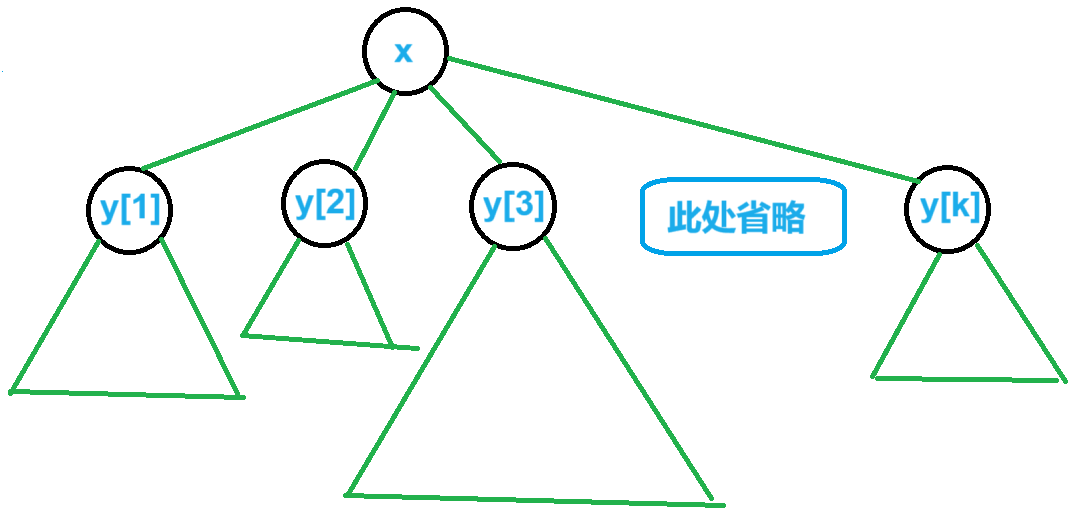
首先，对于 $y_1,y_2,y_3,\cdots,y_k$，明显需要的时间分别是 $dp_{y_1},dp_{y_2},dp_{y_3},\cdots,dp_{y_k}$。

那么假设第 $i$ 个被 $x$ 传递信息的节点是 $dp_{c_i}$，则最终答案就是：

\[\max_{i=1}^k(dp_{c_i}+c_i)\]

$dp_{c_i}+c_i$ 的构成

$dp_{c_i}$：传递子树的时间。
$c_i$：等待和传递的时间。等待了 $c_i-1$ 时刻，传递需要 $1$ 时刻。

那么问题就转换为了：如何安排 $dp_{y_1},dp_{y_2},dp_{y_3},\cdots,dp_{y_k}$ 的顺序，使得 $\max\limits_{i=1}^k(dp_{c_i}+c_i)$ 最小。

这其实就是一个简单贪心，将 $dp_{y_1},dp_{y_2},dp_{y_3},\cdots,dp_{y_k}$ 从大到小排序即可（$c_i$ 从小到大有序）。

证明

令原数列 $dp_{y_1},dp_{y_2},dp_{y_3},\cdots,dp_{y_k}$ 为 $a_1,a_2,a_3,\cdots,a_k$。

那么对于元素 $a_i,a_{i+1}$，当 $a_i=a_{i+1}$ 时，交换顺序显然不影响答案。

当 $a_i>a_{i+1},a_i\geq a_{i+1}+1$ 时：
$$ \max(a_i+i,a_{i+1}+i+1)=a_i+i=\max(a_i,a_{i+1})+i $$
当 $a_i<a_{i+1},a_{i+1}\geq a_i+1$ 时：
$$ \max(a_i+i,a_{i+1}+i+1)=a_{i+1}+i+1=\max(a_i,a_{i+1})+i+1 $$

容易发现，$a_i>a_{i+1}$ 时，$\max(a_i+i,a_{i+1}+i+1)$ 会更小一些，因此对于 $1\leq i<n$，都应当有 $a_i>a_{i+1}$ 更优。

证毕。

复杂度分析

枚举根节点：时间复杂度 $\mathcal O(n)$。

递推一次时间复杂度：$\mathcal O(n)$。

排序的时间复杂度：$\mathcal O\left(n\log n\right)$。

听起来好像是 $\mathcal O\left(n^3\log n\right)$ 的，然而实际上每一次枚举根节点后递推时，并不是每次都会加入 $n$ 个节点，因此不是每一次排序的复杂度都是 $\mathcal O(n\log n)$，而是一共加入了 $n$ 个节点，总排序的时间复杂度不超过 $\mathcal O(n\log n)$。

故：总时间复杂度为 $\mathcal O\left(n^2\log n\right)$，可以通过此题。

AC 代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=1000; 
struct graph{
	struct edge{
		int v,r;
	}a[2*(N-1)+1];
	
	int h[N+1];
	void create(int u,int v){
		static int top;
		a[++top]={v,h[u]};
		h[u]=top;
	}
}g;
//dp[i]:从i(不包括)传递整个i的子树的时间 
int n,ans[N+1],dp[N+1];
bool cmp(int a,int b){
	return a>b;
}
void dfs(int x,int fx){
	vector<int>tmp;
	int top=0;
	for(int i=g.h[x];i>0;i=g.a[i].r){
		if(g.a[i].v==fx)continue;
		dfs(g.a[i].v,x);
		tmp.push_back(dp[g.a[i].v]);
	}
	sort(tmp.begin(),tmp.end(),cmp);
	dp[x]=0;
	for(int i=0;i<tmp.size();i++){
		dp[x]=max(dp[x],tmp[i]+i+1);//注意vector的下标从0开始
	}
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	scanf("%d",&n);
	for(int i=2;i<=n;i++){
		int u;
		scanf("%d",&u);
		g.create(u,i);
		g.create(i,u);
	}
	for(int i=1;i<=n;i++){
		dfs(i,0);
		ans[i]=dp[i]+1;
	}
	int Min=2147483647;
	for(int i=1;i<=n;i++){
		Min=min(Min,ans[i]);
	}
	printf("%d\n",Min);
	for(int i=1;i<=n;i++){
		if(ans[i]==Min){
			printf("%d ",i);
		}
	}
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

题解：消息传递

洛谷P2018