题解 平衡树 Splay 提高+/省选− 基础算法

Splay树详解

例题：洛谷P3369

Posted by TH911 on January 22, 2025

前置知识：平衡树。

例题链接。例题加强版链接。

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

  1. 插入一个数 $x$。
  2. 删除一个数 $x$（若有多个相同的数，应只删除一个）。
  3. 定义排名为比当前数小的数的个数 $+1$。查询 $x$ 的排名。
  4. 查询数据结构中排名为 $x$ 的数。
  5. 求 $x$ 的前驱（前驱定义为小于 $x$，且最大的数）。
  6. 求 $x$ 的后继（后继定义为大于 $x$，且最小的数）。

对于操作 $3,5,6$，不保证当前数据结构中存在数 $x$。

Splay 树核心思路是通过 splay 操作不断将操作节点旋转到根节点，从而保证均摊复杂度 $\mathcal O(\log n)$。

并且，Splay 树其实是 splay 越多越快的，splay 操作次数越多，树的形态也就越平衡。（也就是说，可以尝试随机 splay 几个点，时间消耗可能会有所提升。）

Splay 的各类平衡树操作都是简单的 BST 操作，操作完之后将操作节点 splay 到根节点即可。

Splay 基本结构/操作

以例题为例。

节点维护信息

1
2
3
4

struct node{
    int value,cnt;
    int size,father,child[2];
}t[N+1];

$\textit{value}x$ 为节点实际维护信息，$\textit{cnt}_x$ 为相同节点个数。$\textit{size}_x,\textit{father}_x,\textit{child}{x,0},\textit{child}_{x,1}$ 分别为 $x$ 子树大小、父节点、左子节点、右子节点。

钦定左子树的值均小于右子树的值。

同时，对于整棵平衡树而言，还需要存储整棵树的根节点 root。

辅助操作

1
2
3
4
5
6

void up(int p){
    t[p].size=t[t[p].child[0]].size+t[p].cnt+t[t[p].child[1]].size;
}
bool check(int p){
    return t[t[p].father].child[1]==p;
}

up 操作用于更新子树大小，check 操作用于判断是左子节点还是右子节点，$0$ 表示左子节点，$1$ 表示右子节点。

rotate 操作

如图：

先考虑右旋如何操作。

图中需要将 $1$ 挂到 $2$ 的右子树上，再将 $5$ 挂到 $1$ 的左子树上。

推广到一般情况，需要对节点 $x$ 进行 rotate 操作，记 $y=\textit{father}_x,z=\textit{father}_y$。

则需要断边 $(z,y),(y,x),(x,\textit{child}{x,1})$，连边 $(z,x),(x,y),(y,\textit{child}{x,1})$。且此时 $y$ 为新的 $\textit{child}{x,1}$，原来的 $\textit{child}{x,1}$ 为新的 $\textit{child}_{y,0}$。

注意需要同时更新 $\textit{child}_0,\textit{child}_1$ 和 $\textit{father}$，并且不要影响 $0$ 号节点，需要特判。

显然，右旋是将左子节点旋转上去，左旋是将右子节点旋转上去。且左旋是与右旋相对的，因此可以通过判断 $x$ 是 $\textit{father}_x$ 的左子节点还是右子节点，从而判断是左旋还是右旋。

一定要注意节点信息更改的顺序。记 $y=\textit{father}_x,z=\textit{father}_y$，则修改 $\textit{child}_z$ 之前不应当修改 $y$ 的父节点，否则 check 函数无法正确判断。同时，不要修改 $0$ 节点的信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

void rotate(int x){
    int y=t[x].father,z=t[y].father;
    bool mode=check(x);
    t[y].child[mode]=t[x].child[!mode];
    t[x].child[!mode]=y;
    if(z){
        t[z].child[check(y)]=x;
    }
    if(t[y].child[mode]){
        t[t[y].child[mode]].father=y;
    }
    t[y].father=x; 
    t[x].father=z;
    up(y);
    up(x);
}

splay 操作

splay 操作是 Splay 树的核心操作。如同 FHQ Treap 的 split 操作与 merge 操作。

splay 操作用于将节点 $x$ 通过 rotate 操作旋转至根节点。

假设对 $x$ 进行 splay 操作，记 $p$ 为本次 rotate 操作之前的 $\textit{father}_x$，$g$ 为本次 rotate 操作之前的 $\textit{father}_p$。

zig 与 zag

zig 指代此处的右旋（将左孩子转上去），zag 指代左旋（将右孩子转下来）。

splay 操作中途有三种具体操作：

  • zig 与 zag 操作：当 $p$ 为根节点时，直接 rotate 一次即可。

  • zig-zig 与 zag-zag 操作：当 $p$ 不为根节点，且 $x,p$ 为同侧子节点时，先 rotate 一次 $p$，再 rotate 一次 $x$ 即可。

    如图：

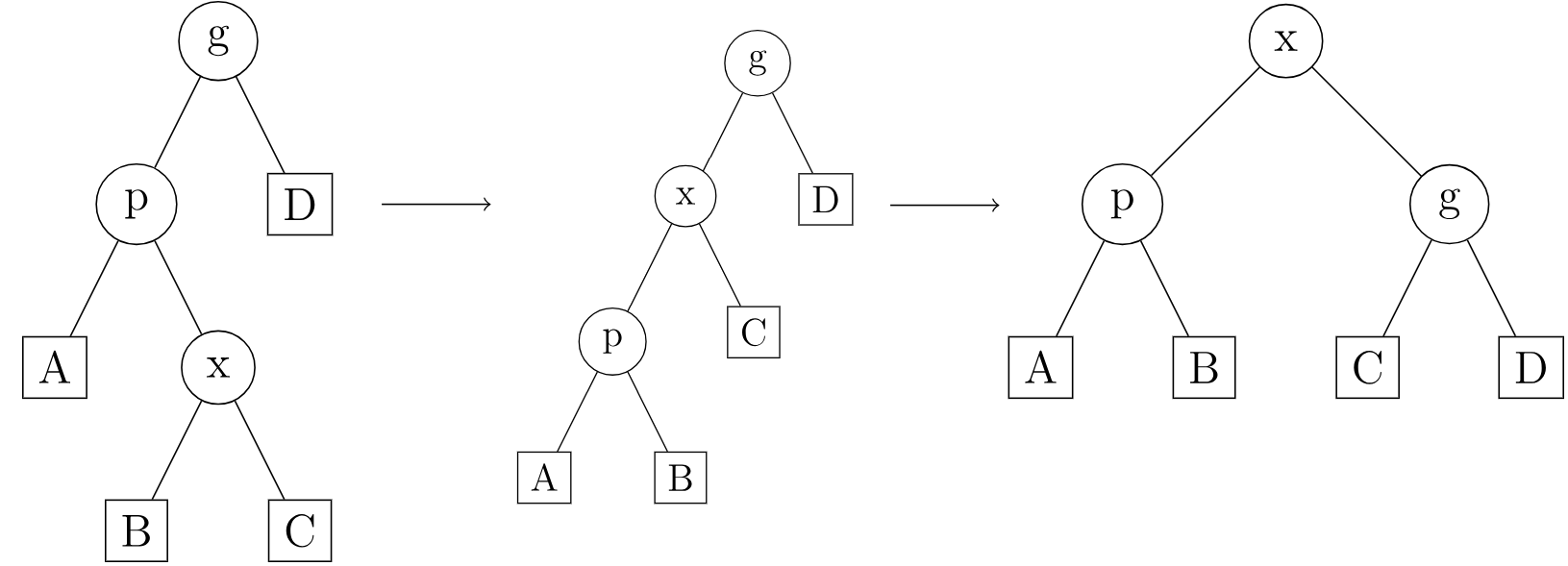
  • zig-zag 与 zag-zig 操作：当 $p$ 不为根节点，且 $x,p$ 为异侧子节点时，先 rotate 一次 $x$，此时 $\textit{father}_x=g$，再 rotate 一次 $x$ 即可。

    如图：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

int splay(int x){
    while(t[x].father){
        int p=t[x].father;
        if(!t[p].father){
            rotate(x);
            break;
        }
        if(check(p)==check(x)){
            rotate(p);
            rotate(x);
        }else{
            rotate(x);
            rotate(x);
        }
    }
    return x;
}

查找元素

Splay 与 FHQ Treap 暴力分裂不同，Splay 的很多操作都是在 BST 上完成的，因此需要在 BST 上查找元素。查找完成后，将其 splay 到根节点，也有利于各种操作的实现。

特别地，若查询值为 $x$ 的节点不存在时，应当查找到其前驱/后继节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

int find(int x){
    int p=root;
    while(true){
        if(t[p].value==x){
            break;
        }else if(x<t[p].value){
            if(!t[p].child[0]){
                break;
            }else{
                p=t[p].child[0];
            }
        }else{
            if(!t[p].child[1]){
                break;
            }else{
                p=t[p].child[1];
            }
        } 
    }
    return root=splay(p);
}

同样不难写出按排名查找的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

int kth(int k,int p=root){
    while(true){
        if(t[t[p].child[0]].size+1<=k&&k<=t[t[p].child[0]].size+t[p].cnt){
            break;
        }else if(k<t[t[p].child[0]].size+1){
            p=t[p].child[0];
        }else{
            k-=t[t[p].child[0]].size+t[p].cnt;
            p=t[p].child[1]; 
        }
    }
    root=splay(p);
    return t[root].value;
}

Splay 平衡树操作

插入节点

比较简单，在 BST 上查找，最终要么找到值同样为 $x$ 的节点，修改 $\textit{cnt}$ 即可；否则最终会找到一个空节点，创建节点并挂到父节点上，再 splay 到根节点即可。

注意插入完成后要进行一次 up 操作。特判空树。

void insert(int x){
    if(!root){
        root=create(x);
        return;
    }
    int p=root;
    while(true){
        if(t[p].value==x){
            t[p].cnt++;
            break;
        }else if(x<t[p].value){
            if(!t[p].child[0]){
                t[p].child[0]=create(x);
                t[t[p].child[0]].father=p;
                p=t[p].child[0];
                break;
            }else{
                p=t[p].child[0];
            }
        }else{
            if(!t[p].child[1]){
                t[p].child[1]=create(x);
                t[t[p].child[1]].father=p;
                p=t[p].child[1];
                break;
            }else{
                p=t[p].child[1];
            }
        }
    }
    up(p);
    root=splay(p);
}

删除节点

通过 find 找到待删除节点，旋转到根节点。

  • 若根节点的值不是待删除节点，结束操作。

  • 否则将 $\textit{cnt}{\textit{root}},\textit{size}{\textit{root}}$ 减去 $1$。

    • 若此时 $\textit{cnt}_{\textit{root}}\neq0$，结束操作。

    • 否则若 $\textit{cnt}_{\textit{root}}=0$，则根节点实际上应当被删除。

      那么此时的两个子节点 $p,q$ 就成为了独立的两棵子树，需要将其合并。钦定子树 $p$ 的值均小于子树 $q$ 的值。

      那么，从子树 $q$ 中找到一个最小值，将其 splay 到 $q$ 的父节点，成为新的 $\textit{root}$ 即可。此时 $p,q$ 分别为 $\textit{root}$ 的左右子节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

void erase(int x){
    find(x);
    if(t[root].value!=x){
        return;
    }
    t[root].cnt--;
    t[root].size--;
    if(t[root].cnt){
        return;
    }
    int p=t[root].child[0],q=t[root].child[1];
    t[p].father=t[q].father=0;
    if(!p||!q){
        root=p|q;
        return;
    }
    kth(1,q);
    t[root].child[0]=p;
    t[p].father=root;
    up(root);
}

查询排名

令待查询节点为 $x$。

首先可以通过 find 找出其 $x$ 或者前驱/后继，并旋转到根节点 $\textit{root}$。

  • 若 $\textit{value}{\textit{root}}<x$，则说明 $\textit{root}$ 是 $x$ 的前驱，因此可以直接得到答案 $\textit{size}{\textit{child}{\textit{root},0}}+\textit{cnt}{\textit{root}}+1$。

  • 否则 $x\leq\textit{value}{\textit{root}}$，则说明左子树 $\textit{child}_{\textit{root},0}$ 内即所有小于 $x$ 的数。因此可以得到答案 $\textit{size}{\textit{child}_{\textit{root},0}}+1$。

1
2
3
4
5
6
7
8

int rank(int x){
    find(x);
    if(t[root].value<x){
        return t[t[root].child[0]].size+t[root].cnt+1;
    }else{
        return t[t[root].child[0]].size+1;
    }
}

查询前驱

首先显然可以 find 一次。若 $\textit{value}{\textit{root}}<x$，则说明 $\textit{root}$ 是 $x$ 的前驱，答案即 $\textit{value}{\textit{root}}$。

否则答案即左子树中的最大值。

1
2
3
4
5
6
7
8
9
10
11
12

int prev(int x){
    find(x);
    if(t[root].value<x){
        return t[root].value;
    }
    int p=t[root].child[0];
    while(t[p].child[1]){
        p=t[p].child[1];
    }
    root=splay(p);
    return t[root].value;
}

查询后继

与查询前驱同理。

1
2
3
4
5
6
7
8
9
10
11
12

int next(int x){
    find(x);
    if(x<t[root].value){
        return t[root].value;
    }
    int p=t[root].child[1];
    while(t[p].child[0]){
        p=t[p].child[0];
    }
    root=splay(p);
    return t[root].value;
}

例题 AC 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=1e5;
struct Splay{
	static int root;
	int size;
	struct node{
		int value,cnt;
		int size,father,child[2];
	}t[N+1];
	
	void up(int p){
		t[p].size=t[t[p].child[0]].size+t[p].cnt+t[t[p].child[1]].size;
	}
	bool check(int p){
		return t[t[p].father].child[1]==p;
	}
	void rotate(int x){
		int y=t[x].father,z=t[y].father;
		bool mode=check(x);
		t[y].child[mode]=t[x].child[!mode];
		t[x].child[!mode]=y;
		if(z){
			t[z].child[check(y)]=x;
		}
		if(t[y].child[mode]){
			t[t[y].child[mode]].father=y;
		}
		t[y].father=x; 
		t[x].father=z;
		up(y);
		up(x);
	}
	int splay(int x){
		while(t[x].father){
			int p=t[x].father;
			if(!t[p].father){
				rotate(x);
				break;
			}
			if(check(p)==check(x)){
				rotate(p);
				rotate(x);
			}else{
				rotate(x);
				rotate(x);
			}
		}
		return x;
	}
	int create(int x){
		t[++size]={x,1,1};
		return size;
	}
	void insert(int x){
		if(!root){
			root=create(x);
			return;
		}
		int p=root;
		while(true){
			if(t[p].value==x){
				t[p].cnt++;
				break;
			}else if(x<t[p].value){
				if(!t[p].child[0]){
					t[p].child[0]=create(x);
					t[t[p].child[0]].father=p;
					p=t[p].child[0];
					break;
				}else{
					p=t[p].child[0];
				}
			}else{
				if(!t[p].child[1]){
					t[p].child[1]=create(x);
					t[t[p].child[1]].father=p;
					p=t[p].child[1];
					break;
				}else{
					p=t[p].child[1];
				}
			}
		}
		up(p);
		root=splay(p);
	}
	int find(int x){
		int p=root;
		while(true){
			if(t[p].value==x){
				break;
			}else if(x<t[p].value){
				if(!t[p].child[0]){
					break;
				}else{
					p=t[p].child[0];
				}
			}else{
				if(!t[p].child[1]){
					break;
				}else{
					p=t[p].child[1];
				}
			} 
		}
		return root=splay(p);
	}
	void erase(int x){
		find(x);
		if(t[root].value!=x){
			return;
		}
		t[root].cnt--;
		t[root].size--;
		if(t[root].cnt){
			return;
		}
		int p=t[root].child[0],q=t[root].child[1];
		t[p].father=t[q].father=0;
		if(!p||!q){
			root=p|q;
			return;
		}
		kth(1,q);
		t[root].child[0]=p;
		t[p].father=root;
		up(root);
	}
	int rank(int x){
		find(x);
		if(t[root].value<x){
			return t[t[root].child[0]].size+t[root].cnt+1;
		}else{
			return t[t[root].child[0]].size+1;
		}
	}
	int kth(int k,int p=root){
		while(true){
			if(t[t[p].child[0]].size+1<=k&&k<=t[t[p].child[0]].size+t[p].cnt){
				break;
			}else if(k<t[t[p].child[0]].size+1){
				p=t[p].child[0];
			}else{
				k-=t[t[p].child[0]].size+t[p].cnt;
				p=t[p].child[1]; 
			}
		}
		root=splay(p);
		return t[root].value;
	}
	int prev(int x){
		find(x);
		if(t[root].value<x){
			return t[root].value;
		}
		int p=t[root].child[0];
		while(t[p].child[1]){
			p=t[p].child[1];
		}
		root=splay(p);
		return t[root].value;
	}
	int next(int x){
		find(x);
		if(x<t[root].value){
			return t[root].value;
		}
		int p=t[root].child[1];
		while(t[p].child[0]){
			p=t[p].child[0];
		}
		root=splay(p);
		return t[root].value;
	}
	void print(int p=root){
		if(!p){
			return;
		}
		print(t[p].child[0]);
		for(int i=1;i<=t[p].cnt;i++){
			cerr<<t[p].value<<' ';
		}
		print(t[p].child[1]);
	}
}t;
int Splay::root;
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	int n;
	cin>>n;
	while(n--){
		int opt,x;
		cin>>opt>>x;
		switch(opt){
			case 1:
				t.insert(x);
				break;
			case 2:
				t.erase(x);
				break;
			case 3:
				cout<<t.rank(x)<<'\n';
				break;
			case 4:
				cout<<t.kth(x)<<'\n';
				break;
			case 5:
				cout<<t.prev(x)<<'\n';
				break;
			case 6:
				cout<<t.next(x)<<'\n';
				break;
		}
	}
	
	cout.flush();
	 
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

Splay 与可持久化

Splay 是不能可持久化的，因为 Splay 的复杂度是基于势能均摊得到的。

只有复杂度严格一致或是期望一致的数据结构才能可持久化。

否则例如 Splay，可以构造一种情况需要将深度为 $\mathcal O(n)$ 的节点 splay 到根节点，可持久化每一次都是这个版本，复杂度就变为了 $\mathcal O(mn)$。

所以还是写 FHQ Treap 吧。

CATALOG
    FEATURED TAGS
    树状数组 题解 提高+/省选− 省选/NOI− DP 普及+/提高 基础算法 数学 组合数学 普及/提高− 贪心 字符串 线段树 未完 图论 平衡树 数论 树形 DP 搜索 Tarjan Trie 二分 位运算 二分答案 状态压缩 FHQ Treap 前端 无聊时候的一点思考 最短路 树链剖分 NOI/NOI+/CTSC
    FRIENDS