前置知识:Trie树
例题:最大异或对
给定 $a_1,a_2,a_3,\cdots,a_n$,求 $a_i\oplus a_j$ 的最大值,其中“$\oplus$”表示异或。
我们先分析一下:当什么时候,$a_i \oplus a_j$ 会尽可能大?
显然,$a_i,a_j$ 在二进制下高位不同时会尽可能大,因为 $2^k>2^{k-1}+2^{k-2}+2^{k-3}+\cdots+2^0$。
因此对于 $a_i$,能够使 $a_i \oplus a_j$ 尽可能大的 $a_j$,一定是高位尽可能不同的。
01Trie 数据结构
众所周知,Trie树是用来存储字符串的,然而我们若是将一个数的二进制视为字符串,同样能够存入Trie中。
即一个字符集为 ${0,1}$ 的 Trie树。
这样的好处就是按照二进制存储。
回顾上文,高位不同,我们在01Trie上从高到低尽可能查找高位不同的数即可(如果没有就选择相同的)。最终路径即使 $a_i \oplus a_j$ 最大的 $a_j$ 的二进制。
此时我们再将 $a_i\oplus a_j$ 算出来即可。
这样查找一次的时间复杂度是 $\mathcal O\left(\log n\right)$ 的,但其实每次都是 $\mathcal O(32)$,因为 int 有 $32$ 位。
那么对于每一个 $a_i$,都这么做一次,最后取最大值,我们就能够在 $\mathcal O\left(n\log n\right)$ 的时间内解决此问题。
AC 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int N=100000;
struct trie{
struct node{
int m[2];
}t[32*N+1];
void insert(int x){
static int top=1;
int p=1;
for(int i=31;i>=0;i--){
int bit=x>>i&1;
if(!t[p].m[bit])t[p].m[bit]=++top;
p=t[p].m[bit];
}
}
int query(int x){
int p=1,ans=0;
for(int i=31;i>=0;i--){
int bit=x>>i&1;
if(t[p].m[!bit]){
p=t[p].m[!bit];
ans|=(!bit)<<i;//注意不要混用逻辑运算符!和位运算符~,~0=111...111,而不是1.
}else{
p=t[p].m[bit];
ans|=bit<<i;
}
}return ans;
}
}trie01;
int n,a[N+1];
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",a+i);
trie01.insert(a[i]);
}
int Max=0;
for(int i=1;i<=n;i++){
Max=max(Max,a[i]^trie01.query(a[i]));
}
printf("%d\n",Max);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
例题:最长异或路径
题目要求在点 $u$ 和点 $v$ 的路径上的权值异或和。
这条路径肯定形如:
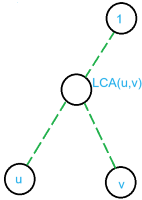
也就是说,$u\sim v$ 的权值异或和为 $u\sim LCA(u,v)$ 的异或和异或上 $LCA(u,v)\sim v$ 的异或和。
令 $f(u,v)$ 表示 $u\sim v$ 的路径上的权值异或和。
考虑到一个原理:$a\oplus a\oplus b=0\oplus b=b$。
则有:
\[\begin{aligned} f(u,v)&=f(u,LCA(u,v))\oplus f(LCA(u,v),v)\\ &=f(1,LCA(u,v))\oplus f(u,LCA(u,v)) \oplus f(1,LCA(u,v))\oplus f(LCA(u,v),v)\\ &=f(1,u)\oplus f(1,v) \end{aligned}\]显然,$f(1,u)$ 和 $f(1,v)$ 都可以预处理出来。
那么这就和上一道例题一模一样了。
AC 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=100000;
struct edge{
int v,r,w;
}a[2*(N-1)+1];
int n,h[N+1],value[N+1];
void create(int u,int v,int w){
static int top;
a[++top]={v,h[u],w};
h[u]=top;
}
void dfs(int x,int fx){
for(int i=h[x];i;i=a[i].r){
if(a[i].v!=fx){
value[a[i].v]=value[x]^a[i].w;
dfs(a[i].v,x);
}
}
}
struct trie{
struct node{
int m[2];
}t[32*N+1];
void insert(int x){
static int top=1;
int p=1;
for(int i=31;i>=0;i--){
int bit=x>>i&1;
if(!t[p].m[bit])t[p].m[bit]=++top;
p=t[p].m[bit];
}
}
void build(){
for(int i=1;i<=n;i++){
insert(value[i]);
}
}
int query(int x){
int p=1,ans=0;
for(int i=31;i>=0;i--){
int bit=x>>i&1;
if(t[p].m[!bit]){
p=t[p].m[!bit];
ans|=(!bit)<<i;
}else{
p=t[p].m[bit];
ans|=bit<<i;
}
}return ans;
}
}trie01;
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%d",&n);
for(int i=1;i<n;i++){
int u,v,w;
scanf("%d %d %d",&u,&v,&w);
create(u,v,w);
create(v,u,w);
}
dfs(1,0);
trie01.build();
int Max=0;
for(int i=1;i<=n;i++){
Max=max(Max,value[i]^trie01.query(value[i]));
}
printf("%d\n",Max);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
平衡树
引入:求前缀中 $\leq x$ 的数的个数。
一眼权值树状数组(或平衡树?)。
然而,这需要离散化,需要离线。
如果不能离散化后离线操作呢?
我们可以使用 01Trie 来完成。
具体而言,就是每一次都在 01Trie 上走 $x$ 的二进制,如果是 $1$,就加上(走 $1$ 之前)当前节点的左子树的权值和即可。