什么是 AC 自动机
这不是一个能让你自动 AC 的机器
这不是一个能让你自动 AC 的机器。
给定文本串 $T$ 和多个模式串 $S_1,S_2,S_3,\cdots,S_n$,求 $n$ 个模式串在文本串中的匹配情况。
匹配情况包括:是否出现、出现几次、出现几种等。
AC 自动机的思想与原理
回顾:KMP 算法与 fail 指针
KMP 之所以高效,可以理解为是充分利用了已经匹配的信息,从而不重复匹配,以此高效。
其中一个很重要的东西就是 fail 指针($next$ 数组、$pre$ 数组)。
而在 AC 自动机中同样如此。
Trie树上查找
先将模式串 $S_1,S_2,S_3,\cdots,S_n$ 存入一个 Trie树。
那么我们在 Trie树上查找文本串 $T$ 即可。
但是这样很明显会有问题:我们需要查找多个。
有没有一种办法能够解决问题呢?fail 指针。
我们先只考虑一个的情况。
那么就是说,在某处匹配失效以后,我们需要找到其 fail 指针对应的节点。
如图:
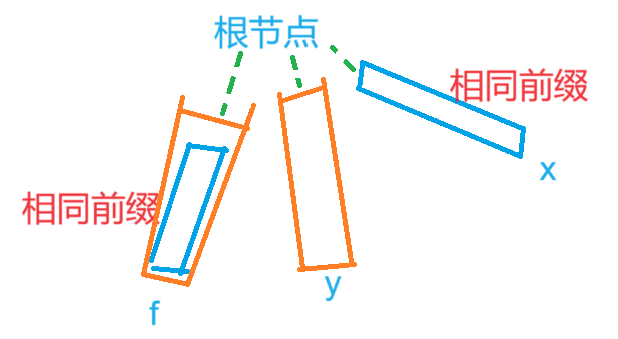
假设我们需要求解 $f$ 的 fail 指针,为了便于分析规定 $dep_f<dep_y<dep_x$,$dep_x$ 表示节点 $x$ 的深度,原因见下文。
首先需要明确的,如果有 $fail[u]=v$,肯定有 $u,v$ 代表的字符相同,且都拥有公共前缀(除非 $v$ 是根节点)。
当 $f$ 失配时,有两个前缀可以找:橙色前缀和蓝色前缀。
而途中也有多个节点:$x,y$ 都拥有相同前缀。
那么到底是 $x$ 还是 $y$ 呢?
与 KMP 不同,AC 自动机的 fail 指针需要支持多个模式串之间的“跳转”,来达到访问其中的一个节点就相当于访问其他节点,而 fail 指针显然不能指向多个节点。
我们可以将 fail 指针构成“链”,跳转之后如果继续失配就继续跳。
在图中就是:例如规定 $fail[f]=x,fail[x]=y$,那么就能够跳到所有的。
那么到底是 $fail[f]=x$ 且 $fail[x]=y$,还是 $fail[f]=y$ 且 $fail[y]=x$ 呢?
回顾 KMP 算法,会发现我们令 border 最长,这样向前跳的距离会短以避免漏掉情况;在这里同样如此。
我们可以令 $fail[y]=x,fail[f]=y$。因为 $y$ 的前缀包括 $x$ 的前缀,所以从 $x$ 跳到 $y$ 是可以的。而 $f$ 的前缀叶包括 $y$ 的前缀,因此这么跳可是可以的。
为什么不从 $y$ 跳到 $f$ 呢?
从 $f$ 跳到 $y$ 能够确保在 BFS 序遍历树的情况下,fail 是确定的(更详细见下文Trie图)。
Trie图
构造 fail 指针时会有一个问题。
从根节点 $0$ 开始构造,构造到了节点 $x$。
由 fail 指针的定义,$x$ 可以看作其父节点的 fail 指针的对应子节点。
要是该子节点不存在呢?
其实也可以循环跳 fail 指针,但是这样效率低,且麻烦。
我们可以将 Trie树改为 Trie图。
具体而言,就是让每一个节点都拥有整个字符集的子节点,然后连边。
比如说字符集为 ${\texttt{a,b,c}}$ ,以 $\texttt{ab}$ 和 $\texttt{bc}$ 构造一棵 Trie树:
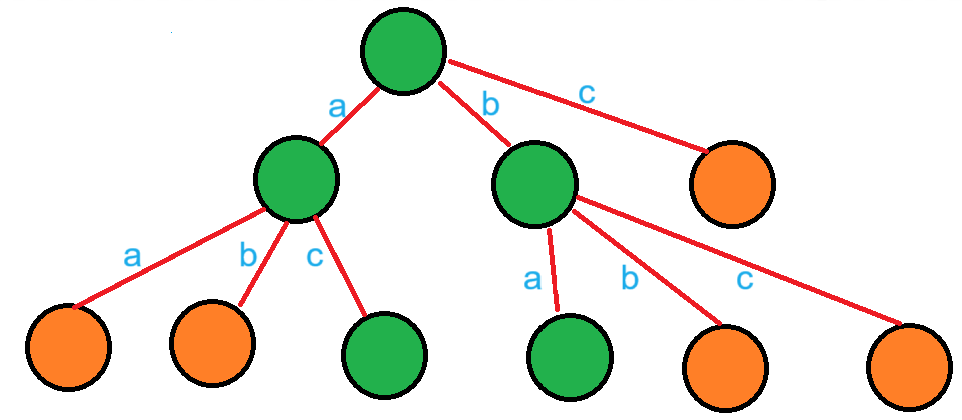
图中橙色节点便是我们“补”的节点。
在构造 fail 指针时,当前节点如果存在,直接递推 fail 指针即可。
否则就是其父节点的 fail 节点的对应节点。
并且考虑到当前节点的 fail 指针都会在当前节点的上一层,因此可以递推。
注意:不存在的“伪”节点不会遍历其子节点,因此复杂度仍然是线性。
拓扑排序:fail 指针“倒树”信息合并
看图:
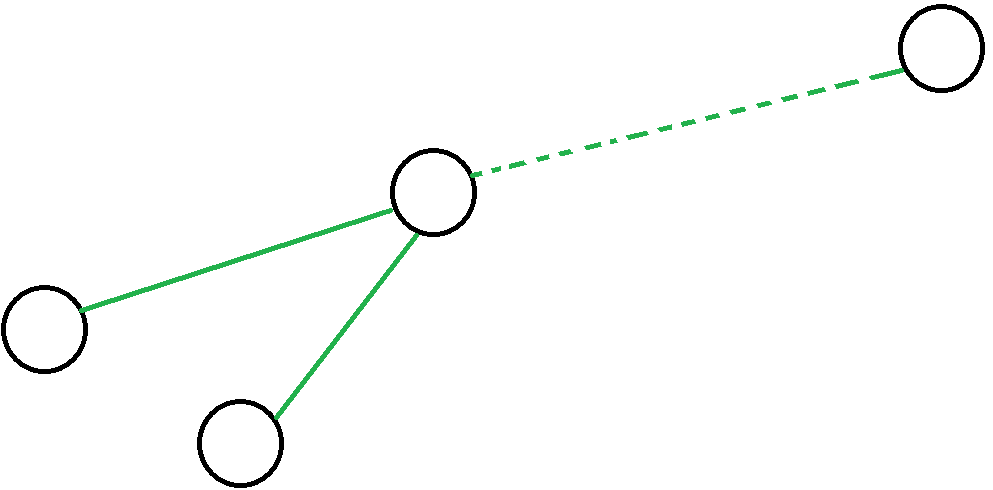
明显的,信息合并的时候,fail 指针会重复跳。
因此我们可以先合并左边两个节点的信息,然后一起合并到 fail 指针的“链”上来优化。
但是如何保证顺序呢?
拓扑排序即可,拓扑排序可以将信息维护变为线性结构。
但其实没有必要再进行一次拓扑排序,因为上文提到了 fail 指针的构建顺序:BFS 序。此处我们将 BFS 序倒过来来合并即可。
这样,整个 fail 指针便构成了一棵“倒树”——每条边都从子节点指向父节点。
【模板】AC 自动机 AC 代码
AC 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
#include<unordered_map>
using namespace std;
typedef unsigned long long ull;
constexpr const int N=2e5,S=2e5,T=2e6;
int n;
int flag[N+1];
unordered_map<string,int>map;
string s;
char t[T+1];
queue<int>q;
struct trie{
struct node{
int m[26];
int id,fail,cnt;
}t[S+1];
int top;
void insert(string s,int id){
int p=0;
for(int i=0;i<s.size();i++){
if(!t[p].m[s[i]-'a'])t[p].m[s[i]-'a']=++top;
p=t[p].m[s[i]-'a'];
}
t[p].id=id;
}
int q[N+1],front,rear;
void build(){//构造 fail 指针
t[0].fail=0;
//注意这里只入队真子节点,伪造的子节点不需要加入队列
for(int i=0;i<26;i++){
if(t[0].m[i]){
t[t[0].m[i]].fail=0;
q[rear++]=t[0].m[i];
}else t[t[0].m[i]].fail=0;
}
while(front<rear){
int u=q[front++];
for(int i=0;i<26;i++){
if(t[u].m[i]){
t[t[u].m[i]].fail=t[t[u].fail].m[i];
q[rear++]=t[u].m[i];
}else t[u].m[i]=t[t[u].fail].m[i];
}
}
}//查询
void query(char *ss){
int p=0;
static int ans[N+1];
memset(ans,0,sizeof(ans));
for(int i=0;ss[i];i++){
p=t[p].m[ss[i]-'a'];
t[p].cnt++;//cnt技术,下文合并信息
}
for(int i=rear-1;i>=0;i--){//id可以找到原来的答案
ans[t[q[i]].id]+=t[q[i]].cnt;
t[t[q[i]].fail].cnt+=t[q[i]].cnt;//合并到fail上,后面fail再统计
}
for(int i=1;i<=n;i++){
if(flag[i]==0)printf("%d\n",ans[i]);
else printf("%d\n",ans[flag[i]]);
}
}
}trie;
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%d",&n);
for(int i=1;i<=n;i++){
cin>>s;
//去重,因为标记.id是直接赋值
if(map.count(s)){
flag[i]=map[s];
}else{
map[s]=i;
trie.insert(s,i);
}
}trie.build();
scanf("%s",t);
trie.query(t);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
[TJOI2013] 单词
很简单,仅仅需要注意的是,“文章”(文本串)就是给定的单词(模式串)中间加上一堆标点符号或空格即可。
那么构造一下文本串为模式串之间用一个非英文小写字母的字符隔开,作 AC 自动机即可。
AC 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
#include<unordered_map>
using namespace std;
typedef unsigned long long ull;
constexpr const int N=1e6,S=1e6;
int n;
int flag[N+1];
unordered_map<string,int>map;
string s,t;
queue<int>q;
struct trie{
struct node{
int m[26];
int id,fail,cnt;
}t[S+1];
int top;
void insert(string s,int id){
int p=0;
for(int i=0;i<s.size();i++){
if(!t[p].m[s[i]-'a'])t[p].m[s[i]-'a']=++top;
p=t[p].m[s[i]-'a'];
}
t[p].id=id;
}
int q[N+1],front,rear;
void build(){
t[0].fail=0;
for(int i=0;i<26;i++){
if(t[0].m[i]){
t[t[0].m[i]].fail=0;
q[rear++]=t[0].m[i];
}else t[t[0].m[i]].fail=0;
}
while(front<rear){
int u=q[front++];
for(int i=0;i<26;i++){
if(t[u].m[i]){
t[t[u].m[i]].fail=t[t[u].fail].m[i];
q[rear++]=t[u].m[i];
}else t[u].m[i]=t[t[u].fail].m[i];
}
}
}
void query(string ss){
int p=0;
static int ans[N+1];
memset(ans,0,sizeof(ans));
for(int i=0;i<ss.size();i++){
p=t[p].m[ss[i]-'a'];
t[p].cnt++;
}
for(int i=rear-1;i>=0;i--){
ans[t[q[i]].id]+=t[q[i]].cnt;
t[t[q[i]].fail].cnt+=t[q[i]].cnt;
}
for(int i=1;i<=n;i++){
if(flag[i]==0)printf("%d\n",ans[i]);
else printf("%d\n",ans[flag[i]]);
}
}
}trie;
int main(){
// freopen("test.in","r",stdin);
// freopen("test.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++){
cin>>s;
t+=s+'?';
if(map.count(s)){
flag[i]=map[s];
}else{
map[s]=i;
trie.insert(s,i);
}
}trie.build();
trie.query(t);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}