题意分析
首先,看到 border,我们自然而然地想到了 KMP。
所谓 border,其实就是其前缀和后缀相等。
现在,给定了字符串 $s$,求 $s[1,p]$ 和 $s[1,q]$ 的最长公共 border。($s[l,r]$ 表示 $s$ 中第 $l$ 位到第 $r$ 组成的字符串)
我们先考虑如何求出 border。
参照 KMP 算法即可。(如果你不会 KMP 算法:link)。
KMP 一遍后求出了 $pre$ 数组。
然后呢?
我们先绘制一张图。
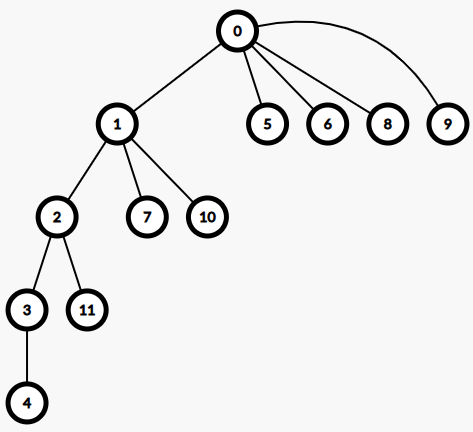
这是通过样例 $1$ 的字符串的 $pre$ 数组画出的树,比如说 $pre_4=3,pre_5=0,pre_2=1,\cdots$。
(参见此处,本文中的 KMP 算法的字符串下标从 $1$ 开始,则特殊值取 $0$)
举个例子:$s[1,7]$ 和 $s[1,10]$ 都是 $s$ 的 border,而 $s[1,1]$ 却是 $s$ 的 border 的同时也是 $s[1,7]$ 和 $s[1,10]$ 的公共 border。
那么如此,我们便通过 $pre_i$ 建立了一棵树,$pre_i$ 就是 $i$ 的父节点。
求 $s[1,p]$ 和 $s[1,q]$ 的最长公共 border 即 LCA 问题。
AC 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int N=1e6;
char a[N+1];
int n,pre[N+1],d[N+1],f[N+1][__lg(N+1)+1],lg[N+1];
void solve(){
d[1]=1;
for(int i=2,j=0;i<=n;i++){//KMP
while(j!=0&&a[j+1]!=a[i])j=pre[j];
if(a[j+1]==a[i])j++;
pre[i]=j;
d[i]=d[j]+1;
}
for(int i=1;i<=n;i++)f[i][0]=pre[i];
for(int i=1;i<=n;i++)lg[i]=lg[i>>1]+1;//常数优化
for(int i=1;i<=n;i++)lg[i]--;
for(int i=1;i<=lg[n];i++){
for(int x=1;x<=n;x++)f[x][i]=f[f[x][i-1]][i-1];
}
}//倍增LCA
int lca(int u,int v){
if(d[u]<d[v])swap(u,v);
for(int i=lg[d[u]-d[v]];i>=0;i--){
if(d[f[u][i]]>=d[v])u=f[u][i];
}
for(int i=lg[d[u]];i>=0;i--){
if(f[u][i]!=f[v][i])u=f[u][i],v=f[v][i];
}return f[u][0];
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%s",a+1);
n=strlen(a+1);
solve();
int m;
scanf("%d",&m);
while(m--){
int p,q;
scanf("%d %d",&p,&q);
printf("%d\n",lca(p,q));
}
/*fclose(stdin);
fclose(stdout);*/
return 0;
}