实话实说,真不觉得能够评蓝……
$2025/7/20$ 更新:好了,降黄了……
$\mathcal O\left(n\right)$ 做法
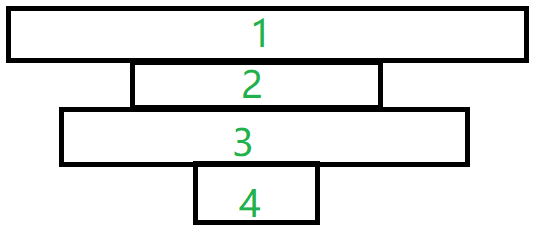
如图,如果一个盘子能够通过第 $2$ 个管道,那么其宽度一定小于第 $2$ 个管道的深度,也就小于了第 $3$ 个管道的宽度。那么我们就可以把原序列变为一个单调不升序列(如图):
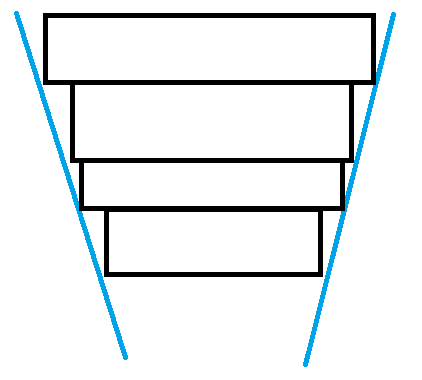
在此之后,我们就可以用一个指针 $pl$ 来判定当前盘子最多会掉到哪一层,每次模拟即可。
总时间复杂度:$\mathcal O\left(n+m\right)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int N=300000,M=300000;
int n,m,r[N+1]={2147483647},k[M+1];
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",r+i);
r[i]=min(r[i],r[i-1]);
}
for(int i=1;i<=m;i++)scanf("%d",k+i);
int pl=n;
for(int i=1;i<=m&&pl>=0;i++){
while(k[i]>r[pl])pl--;
pl--;
}printf("%d\n",pl+1);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
$\mathcal O\left(n\log_2n\right)$ 做法
二分
和$\mathcal O\left(n\right)$ 做法 一样,先将原序列变为一个单调不升序列。
随后在序列上进行二分来查找会被哪一个管道卡住即可。
找到了以后就丢弃其下的,因为剩下的盘子不可能放到这个盘子之下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int N=300000,M=300000;
int n,m,R[N+1]={2147483647};
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",R+i);
R[i]=min(R[i],R[i-1]);
}int pl=n;
for(int i=1;i<=m&&pl>0;i++){
int k;
scanf("%d",&k);
int x,l=1,r=pl;
while(l<r){
int mid=(l+r)>>1;
if(R[mid]>=k)x=mid,l=mid+1;
else r=mid-1;
}if(pl==x)pl--;
else pl=x;
}printf("%d\n",pl);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}