题意分析
当 $a_i$ 对答案产生贡献时,当且仅当存在区间 $[l,r]$ 满足 $i\in[l,r]$ 且 $a_i$ 是 $[l,r]$ 的次大值。
由此我们开始做题。
计算合法区间数
显然,当且仅当区间中有且仅有一个数大于 $a_i$ 时,答案会增加 $a_i$。
那么我们考虑算出,对于每一个 $a_i$,会造成多少个 $a_i$ 的贡献。
如果我们找出了 $a_i$ 左右两边第一个、第二个大于 $a_i$ 的数,从左至右分别记作 $a_{dl_i},a_{l_i},a_{r_i},a_{dr_i}$(满足 $dl_i<l_i<i<r_i<dr_i$ 且 $ a_{dl_i},a_{l_i},a_{r_i},a_{dr_i}>a_i$),那么这四个数中肯定只能有一个和 $a_i$ 处于同一个区间(否则 $a_i$ 不为次大值)。
那么我们所需要的会对答案造成贡献的区间就不会包含 $a_{dl_i}$ 和 $a_{dr_i}$(因为一旦包含 $a_{dl_i}$,就一定会包含 $d_{l_i}$,$r_i,dr_i$ 同理)。
既然如此,令合法区间为 $[L,R]$,合法情况就只有两种:
- $L\in[dl_i+1,l_i],R\in[i,r_i-1]$,区间包含了 $l_i$,记作 $[L_1,R_1]$。
- $L\in[l_i+1,i],R\in[r_i,dr_i-1]$,区间包含了 $r_i$,记作 $[L_2,R_2]$。
图示:
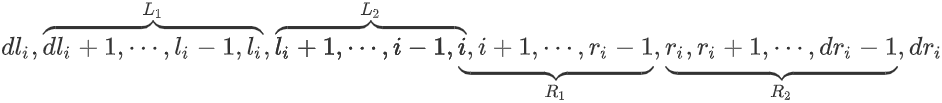
当 $L\in[dl_i+1,l_i],R\in[i,r_i-1]$ 时,则合法区间数为 $\left(l_i-\left(dl_i+1\right)+1\right)\left(\left(r_i-1\right)-i+1\right)=(l_i-dl_i)(r_i-i)$。
同样地,当 $L\in[l_i+1,i],R\in[r_i,dr_i-1]$ 时,合法区间数为 $\left(i-l_i\right)\left(dr_i-r_i\right)$。
那么 $a_i$ 对答案的总贡献就是 $a_i\times\left[\left(l_i-dl_i\right)\left(r_i-i\right)+\left(i-l_i\right)\left(dr_i-r_i\right)\right]$,可以 $\mathcal O\left(1\right)$ 求解。
则最终答案为 $\large \sum\limits_{i=1}^n{a_i\times\left[\left(l_i-dl_i\right)\left(r_i-i\right)+\left(i-l_i\right)\left(dr_i-r_i\right)\right]}$(下标从 $1$ 开始)。
但这时我们需要注意的是,这四个数都有可能不会存在,那么初值就变得十分重要,甚至会影响最终答案的正确性。当然,你不嫌麻烦你特判也行。
-
如果你的下标从 $1$ 开始:
1 2 3 4
for(int i=1;i<=n;i++){ l[i]=dl[i]=0; r[i]=dr[i]=n+1; }
-
如果你的下标从 $0$ 开始:
1 2 3 4
for(int i=0;i<n;i++){ l[i]=dl[i]=-1; r[i]=dr[i]=n; }
(其实就是类似于“值域两端”)
解释一下为什么:(下标从 $1$ 开始,从 $0$ 开始和从 $1$ 开始差不多,不能理解可以手推或参见上图)
以 $l_i,dl_i$ 为例,$r_i,dr_i$ 同理可得。
首先,$l_i=dl_i=0$ 的好处就是选取区间时 $l_i+1=dl_i+1=1$(不存在的话)。
如果 $l_i$ 不存在,那么 $dl_i$ 绝对不存在:$l_i=dl_i=1,l_i-dl_i=0$,上文中 $[L_1,R_1]$ 的区间因为要选取 $l_i$ 自然不存在,正确;对于 $[L_2,R_2]$,已经在右边选取了 $r_i$,$l_i$ 自然不会选取到,不影响答案。
如果 $l_i$ 存在,$dl_i$ 不存在:$[L_1,R_1]$ 选取了 $l_i$,则 $1\sim l_i$ 都可以选取,此时 $l_i-dl_i=l_i-0=l_i$,正确;对于 $[L_2,R_2]$,同样与 $l_i,dl_i$ 无关,不影响答案。
这样,我们便可以 $\mathcal O\left(n\right)$ 求出最终答案。
如何计算四个数的位置
说了这么多,我们还是不知道如何求出 $dl_i,l_i,r_i,dr_i$。
事实上,我们仅仅需要从大至小向 set 中加入 $a_i$,然后利用前驱、后继节点来判断大小关系即可。
令 $p_i$ 表示 $a_i$ 的下标,那么按照 $a_i$ 值排序,使得 $\large a_{p_1}>a_{p_2}>a_{p_3}>\cdots>a_{p_n}$。
这时我们用 $i$ 遍历 $[1,n]$,每次在 set 中执行 lower_bound(p[i])(或者 upper_bound(p[i]) 也行,因为 $p_i$ 不重复),找到第一个大于 $p_i$ 的下标 $p_x$。
那么 $p_x$ 在 $p_i$ 之前插入 set,代表 $a_{p_x}>a_{p_i}$,又有 $p_x>p_i$ 且 $p_x$ 最小,则 $p_x=r_{p_i}$。
而 $dr_{p_i}$ 也很简单,当 $p_x$ 不为 set 的最后一个元素(不然越界)时,找到 $p_x$ 的后继节点即可。由 set 的有序特性且 $p_i$ 不重复,$p_x$ 的后继节点就是最小的大于 $p_x$ 的元素 $p_{x’}$,$dr_{p_i}=p_{x’}$。
对于 $l_{p_i}$,其实就是 $p_{x}$ 的前驱节点 $p_y$。因为 set 内 $p_i$ 不重复、$p_x$ 最小且 $p_y<p_x,p_x>p_i$,有 $p_y<p_i$ 且 $p_y$ 最大。
那么就有 $l_{p_i}=p_y$。和 $dr_{p_i}$ 同理,$dl_{p_i}$ 为 $p_y$ 的前驱节点 $p_{y’}$。
注意判定越界。
最后记得将 $p_i$ 插入 set 即可。
不会有人不会求后继节点、前驱节点吧?
使用 next() 和 prev() 即可。
虽然说对迭代器进行自减运算、自加运算,或者进行数学运算后强制类型转换也行,但是确实没有这两个简单。
注意事项
- $dl_i,l_i,r_i,dr_i$ 的初始值。
- 开
long long。
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
#include<set>
using namespace std;
typedef long long ll;
const int N=2e5;
ll n,a[N+1],p[N+1],l[N+1],dl[N+1],r[N+1],dr[N+1];
bool cmp(ll x,ll y){
if(a[x]!=a[y])return a[x]>a[y];
return x<y;
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%lld",&n);
for(ll i=1;i<=n;i++)scanf("%lld",a+i);
for(ll i=1;i<=n;i++){
p[i]=i;
l[i]=dl[i]=0;
r[i]=dr[i]=n+1;
}sort(p+1,p+n+1,cmp);
set<ll>s;
for(ll i=1;i<=n;i++){
auto pl=s.lower_bound(p[i]);
if(pl!=s.end()){
r[p[i]]=*pl;
if(next(pl)!=s.end())dr[p[i]]=*next(pl);
}if(pl!=s.begin()){
pl--;
l[p[i]]=*pl;
if(pl!=s.begin())dl[p[i]]=*prev(pl);
}s.insert(p[i]);
}ll ans=0;
for(ll i=1;i<=n;i++)ans+=a[i]*((l[i]-dl[i])*(r[i]-i)+(i-l[i])*(dr[i]-r[i]));
printf("%lld\n",ans);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}