例题链接

本文所指的“树链剖分”，均指“重链剖分”，即将子树最大的子节点作为重子节点的树链剖分。

由于树链剖分代码较为冗长，本文所有代码均使用命名空间，g 代表邻接表，hld 代表树链剖分，seg 代表线段树。

关于树链剖分

是什么

顾名思义，将一个树剖分为多条链。

为什么

这样可以将原本树上的一对多信息关系化为一对一的线性关系，便于维护。（详见下文）

特点

将树剖分为至多 $\mathcal O(\log n)$ 条链。
每一条链上的 DFS 序均为连续的。

作用

修改 树上两点之间的路径上 所有点的值。
查询 树上两点之间的路径上 节点权值的 和/极值/其它（在序列上可以用数据结构维护，便于合并的信息）。
求解 LCA。
……

概念

首先，我们要知道两个概念：

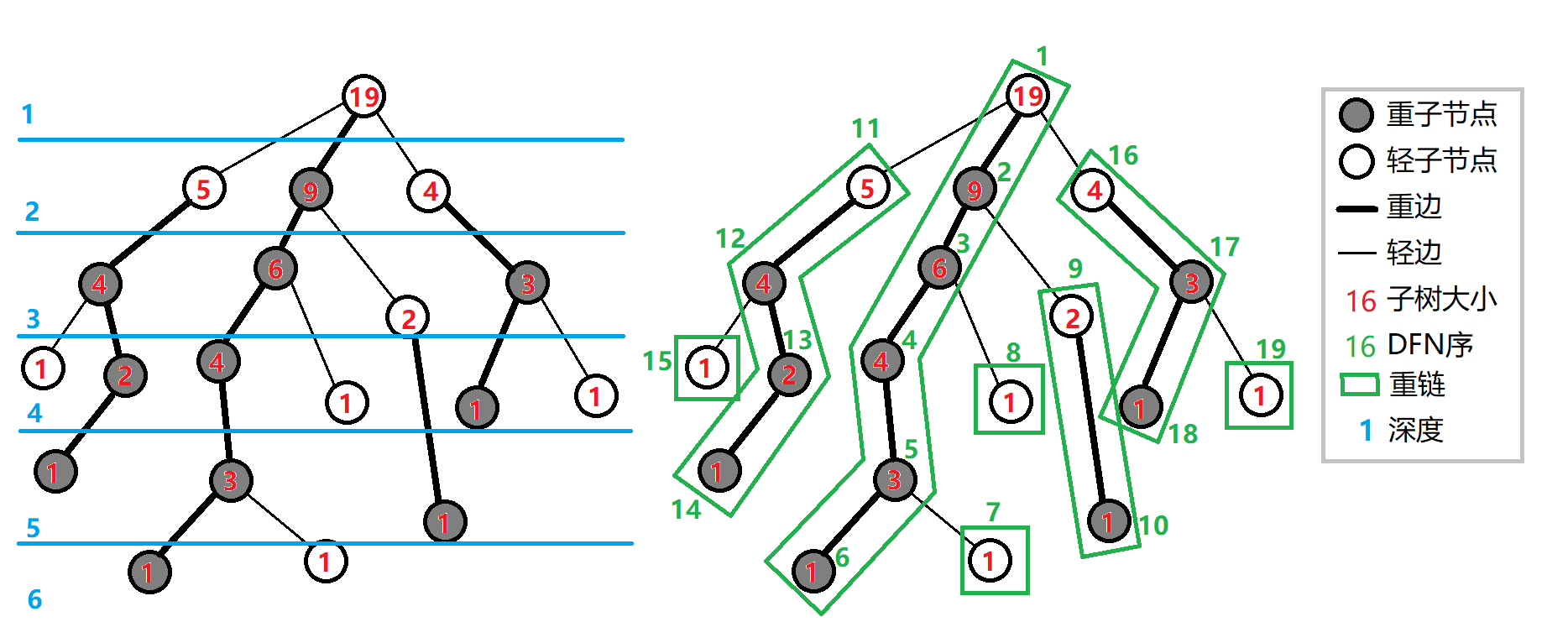
重子节点：一个节点的所有子节点中，子树最大的子节点被称为该节点的“重子节点”。
轻子节点：一个节点除了重子节点的子节点。
重边：连接两个重子节点的边。
轻边：节点连接轻子节点的边。
重链：多条重边两两首尾相连连成的链。

那么树链剖分所剖出来的是什么呢？是 $\mathcal O\left(\log n\right)$ 条重链。

然而，这样势必会有节点“落单”，即不在任何一条重链内。这往往是因为那个节点是叶节点。

叶节点的父节点如果有多个子节点的话，那么必然会有节点不会被连接。

因此，我们将这种落单的节点同样视为一条重链。

所得如图：

图片来源：OI Wiki

实现（预处理）

所需信息

我们需要知道什么呢？

对于节点 $x$，我们需要知道：

$x$ 的子树大小 $\textit{size}_x$，用于判断重子节点是谁；
$x$ 的重子节点 $\textit{son}_x$，作为剖分的依据；
$x$ 的父节点 $f_x$ 与 $x$ 的深度 $d_x$，这是几乎所有树上算法都需要的，用处见后文；
$x$ 所在链的顶部节点（深度最小的节点）$\textit{top}_x$，用处见后文；
$x$ 在 DFS 序中的排名 $\textit{dfn}_x$，用处见后文；
DFS 序对应的节点编号 $\textit{rnk}_{\textit{dfn}_x}=x$，用处见后文；

第一遍 DFS

求出基本信息 $f_x,d_x,\textit{size}_x,\textit{son}_x$。

这并不难，直接看代码：

namespace hld{
	int f[N+1],d[N+1],size[N+1],son[N+1];
	void dfs1(int x,int fx){//fx:x的父节点
		f[x]=fx;
		d[x]=d[fx]+1;
		size[x]=1;
		for(int i=g::h[x];i>0;i=g::a[i].r){
			if(g::a[i].v==fx)continue;
			dfs1(g::a[i].v,x);
			size[x]+=size[g::a[i].v];
			if(size[g::a[i].v]>size[son[x]])son[x]=g::a[i].v;
		}
	}
    //...
}

注意不要在计算 $size_x$ 时漏掉了 $x$ 本身，这虽然可能对求解 $son_x$ 没有影响，但是会对后文维护子树信息有影响。

第二遍 DFS

求解 $\textit{top}_x,\textit{dfn}_x,\textit{rnk}_x$。

与第一遍 DFS 不同，这一次 DFS，其主要目的是对树进行剖分。

定义 $\textit{dfs}2(x,\textit{topx})$，表示 $x$ 在以 $\textit{topx}$ 为顶部节点的链上。

那么就有 $\textit{top}_x=\textit{topx}$。

然后弄一个静态变量作为计数器 $\textit{cnt}$，每次让 $\textit{cnt}\leftarrow \textit{cnt}+1,\textit{dfn}_x\leftarrow \textit{cnt},\textit{rnk}_{\textit{cnt} }\leftarrow x$ 即可。（$\leftarrow$ 表示赋值）

我们需要保证每一条重链上的 DFS 序是连续的（原因见下文），因此优先进行 $\textit{dfs}2(\textit{son}_x,\textit{topx})$。

int top[N+1],dfn[N+1]/*,rnk[N+1]*/;//关于rnk为什么注释：参见后文
void dfs2(int x,int topx){
    top[x]=topx;
    static int cnt;
    dfn[x]=++cnt;
    rnk[cnt]=x;
    if(son[x])dfs2(son[x],topx);
    for(int i=g::h[x];i>0;i=g::a[i].r){
        if(g::a[i].v==f[x]||g::a[i].v==son[x])continue;
        dfs2(g::a[i].v,g::a[i].v);
    }
}

预处理时间复杂度：$\mathcal O(n)$。

至此，树剖就已经完成了，接下来看应用。

应用

例题：洛谷P3384

维护路径信息

对应例题的操作 $1,2$。

事实上，考虑到链上的 DFS 序是连续的，我们完全可以将其看作一个区间来进行维护。

那么，我们就可以使用线段树或是树状数组。

什么时候能够使用树状数组

树状数组能够实现的功能线段树都能够实现。但是树状数组常数更小且更好写。一般来讲，使用树状数组当且仅当能够进行“区间减法”，比如维护区间和，二者都可以：线段树直接查询 $[l,r]$，而树状数组用 $[1,r]$ 减去了 $[1,l-1]$。而维护区间最大值就不能够使用树状数组，因为最大值不能够进行“区间减法”。对于树链剖分，你如果真的想使用树状数组也可以。参见洛谷P2357，树链剖分需要线段树进行区间修改和区间查询，而树状数组要么单点修改区间查询，要么区间修改单点查询（维护差分数组），因此可以考虑像P2357一样维护两个树状数组。

本文使用线段树实现。

首先，我们肯定是需要将 $u\sim v$ 的路径分为 $u\sim \operatorname{lca}(u,v),\operatorname{lca}(u,v)\sim v$ 这两条路径的，那么我们是否需要先求出 $\operatorname(u,v)$ 呢？

不需要。

我们其实仅仅需要当 $u,v$ 不在同一条链时以链为单位向上跳，跳到同一链内后区间修改他们之间差的部分就行了。

路径上修改参考代码：

void add(int u,int v,int k){
    k%=P;
    while(top[u]!=top[v]){
        if(d[top[u]]<d[top[v]])swap(u,v);//防止跳多了
        seg::add(1,dfn[top[u]],dfn[u],k);
        u=f[top[u]];//跳到下一条链
    }if(d[u]>d[v])swap(u,v);
    seg::add(1,dfn[u],dfn[v],k);
}

对应的路径上查询代码：

int query(int u,int v){
    int ans=0;
    while(top[u]!=top[v]){
        if(d[top[u]]<d[top[v]])swap(u,v);
        ans+=seg::query(1,dfn[top[u]],dfn[u]);
        ans%=P;
        u=f[top[u]];
    }if(d[u]>d[v])swap(u,v);
    ans+=seg::query(1,dfn[u],dfn[v]);
    return ans%P;
}

维护子树信息

对应例题的操作 $3,4$。

这甚至于比路径上维护还要简单。

因为明显以 $x$ 为根节点的子树内 DFS 序是连续的，就是 $\textit{dfn}_x\sim \textit{dfn}_x+\textit{size}_x-1$，那么我们区间修改即可。

子树修改代码：

void add(int x,int k){
    k%=P;
    seg::add(1,dfn[x],dfn[x]+size[x]-1,k);
}

子树查询代码：

int query(int x){
    return seg::query(1,dfn[x],dfn[x]+size[x]-1);
}

求解 LCA 问题

其实和维护路径信息一模一样。

拿过来以后删掉一点内容即可。

int lca(int u,int v){
    while(top[u]!=top[v]){
        if(d[top[u]]<d[top[v]])swap(u,v);
        u=f[top[u]];
    }if(d[u]>d[v])swap(u,v);
    return u;
}

例题 AC 代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int N=1e5;
int n,s,P,value[N+1];
namespace g{
	struct edge{
		int v,r;
	}a[2*(N-1)+1];
	int h[N+1];
	void create(int u,int v){
		static int top;
		a[++top]={v,h[u]};
		h[u]=top;
	}
}
namespace hld{
	int rnk[N+1];
}
namespace seg{
	struct node{
		int l,r;
		int sum,tag;
	}t[4*N+1];
	int size(int p){
		return t[p].r-t[p].l+1;
	}
	void up(int p){
		t[p].sum=t[p<<1].sum+t[p<<1|1].sum;
		t[p].sum%=P;
	}
	void build(int p,int l,int r){
		t[p].l=l,t[p].r=r;
		if(l==r){
			t[p].sum=value[hld::rnk[l]]%P;
			return;
		}int mid=(l+r)>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		up(p);
	}
	void down(int p){
		if(t[p].tag){
			t[p<<1].sum+=size(p<<1)%P*t[p].tag;
			t[p<<1].sum%=P;
			t[p<<1].tag+=t[p].tag;
			t[p<<1].tag%=P;
			t[p<<1|1].sum+=size(p<<1|1)%P*t[p].tag;
			t[p<<1|1].sum%=P;
			t[p<<1|1].tag+=t[p].tag;
			t[p<<1|1].tag%=P;
			t[p].tag=0;
		}
	}
	void add(int p,int l,int r,int k){
		if(l<=t[p].l&&t[p].r<=r){
			t[p].sum+=size(p)*k;
			t[p].sum%=P;
			t[p].tag+=k;
			t[p].tag%=P;
			return;
		}down(p);
		if(l<=t[p<<1].r)add(p<<1,l,r,k);
		if(t[p<<1|1].l<=r)add(p<<1|1,l,r,k);
		up(p);
	}
	int query(int p,int l,int r){
		if(l<=t[p].l&&t[p].r<=r)return t[p].sum;
		down(p);
		int ans=0;
		if(l<=t[p<<1].r)ans+=query(p<<1,l,r);
		if(t[p<<1|1].l<=r)ans+=query(p<<1|1,l,r);
		return ans%P;
	}
}
namespace hld{
	int f[N+1],d[N+1],size[N+1],son[N+1];
	void dfs1(int x,int fx){
		f[x]=fx;
		d[x]=d[fx]+1;
		size[x]=1;
		for(int i=g::h[x];i>0;i=g::a[i].r){
			if(g::a[i].v==fx)continue;
			dfs1(g::a[i].v,x);
			size[x]+=size[g::a[i].v];
			if(size[g::a[i].v]>size[son[x]])son[x]=g::a[i].v;
		}
	}int top[N+1],dfn[N+1]/*,rnk[N+1]*/;
	void dfs2(int x,int topx){
		top[x]=topx;
		static int cnt;
		dfn[x]=++cnt;
		rnk[cnt]=x;
		if(son[x])dfs2(son[x],topx);
		for(int i=g::h[x];i>0;i=g::a[i].r){
			if(g::a[i].v==f[x]||g::a[i].v==son[x])continue;
			dfs2(g::a[i].v,g::a[i].v);
		}
	}
	void pre(){
		dfs1(s,0);
		dfs2(s,s);
		seg::build(1,1,n);
	}
	void add(int u,int v,int k){
		k%=P;
		while(top[u]!=top[v]){
			if(d[top[u]]<d[top[v]])swap(u,v);
			seg::add(1,dfn[top[u]],dfn[u],k);
			u=f[top[u]];
		}if(d[u]>d[v])swap(u,v);
		seg::add(1,dfn[u],dfn[v],k);
	}
	int query(int u,int v){
		int ans=0;
		while(top[u]!=top[v]){
			if(d[top[u]]<d[top[v]])swap(u,v);
			ans+=seg::query(1,dfn[top[u]],dfn[u]);
			ans%=P;
			u=f[top[u]];
		}if(d[u]>d[v])swap(u,v);
		ans+=seg::query(1,dfn[u],dfn[v]);
		return ans%P;
	}
	void add(int x,int k){
		k%=P;
		seg::add(1,dfn[x],dfn[x]+size[x]-1,k);
	}
	int query(int x){
		return seg::query(1,dfn[x],dfn[x]+size[x]-1);
	}
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	int m;
	scanf("%d %d %d %d",&n,&m,&s,&P);
	for(int i=1;i<=n;i++)scanf("%d",value+i);
	for(int i=1;i<n;i++){
		int x,y;
		scanf("%d %d",&x,&y);
		g::create(x,y);g::create(y,x);
	}hld::pre();
	while(m--){
		int op,x,y,z;
		scanf("%d",&op);
		switch(op){
			case 1:
				scanf("%d %d %d",&x,&y,&z);
				hld::add(x,y,z);
				break;
			case 2:
				scanf("%d %d",&x,&y);
				printf("%d\n",hld::query(x,y));
				break;
			case 3:
				scanf("%d %d",&x,&z);
				hld::add(x,z);
				break;
			case 4:
				scanf("%d",&x);
				printf("%d\n",hld::query(x));
				break;
		}
	}
	
	fclose(stdin);
	fclose(stdout);
	return 0;
}

树剖复杂度证明

即证明重链数量为 $\mathcal O(\log n)$ 条。

因为重子节点的性质，跳一次轻边子树大小至少会翻倍。因此轻边至多有 $\mathcal O(\log n)$ 条，进而有重链有 $\mathcal O(\log n)$ 条。

树链剖分详解

重链剖分 | 例题：洛谷P3384