本题是错题,后来被证明没有靠谱的多项式复杂度的做法。测试数据非常的水,各种玄学做法都可以通过,不代表算法正确。因此本题题目和数据仅供参考。
题意分析
首先,$p=n-1$。输入时直接 scanf("%d %*d",&n); 即可。
将可能的传播途径视作一棵以节点 $1$ 为根节点的树,那么我们优先救子树最大的节点及其子树。
但是这样会被如下数据卡:
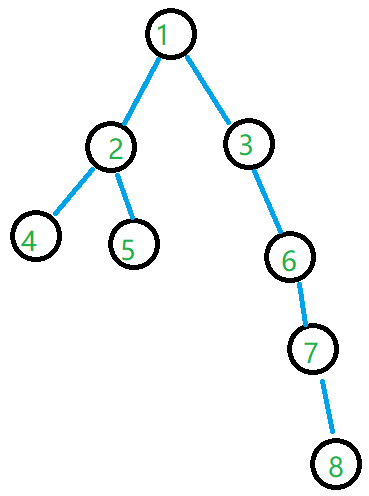
节点 $3$ 的子树大于节点 $2$ 的子树,如果切断 $(1,3)$,那么 $2$ 会死掉,然后 $4,5$ 间必死一个,一共死掉 $3$ 个。
但是,切断 $(1,2)$,$3$ 会死掉,之后再切断 $(3,6)$,则一共死掉 $2$ 个。
这时候可能就会有疑问了:子树最大贪心是错误的?
我们考虑子节点数量最多而不是子树最大,然而依旧会被卡。
怎么办呢?
随机化贪心
模板
顾名思义,在贪心决策中加入随机化。
为了保证最终决策的正确性,执行多次随机化贪心。
模板如下:
1
2
3
4
5
6
7
8
void solve(){
//...
}
//...
while(clock()<CLOCKS_PER_SEC*0.9){
solve();
}//输出答案
//...
其中,clock() 是程序自启动起过了多少个CPU tick,CLOCKS_PER_SEC 是CPU每秒有多少tick
也就是这个 while() 会执行约 $0.9s$,剩下 $0.1s$ 防止 $\text{TLE}$。
关于本题
一个非常简单粗暴的方式,众所周知,rand()%2 会返回 $0$ 或 $1$,那么我们在判断子树最大选择该节点是加上 &&rand()%2 即可。
即使成功的概率微乎其微,但是随机化贪心运行的次数同样多。
自测能跑约 $8\times10^5\sim10^6$ 次随机化贪心。
那么先 DFS 一遍处理出子树大小 $size_i$,然后随机化贪心函数 solve() 内部模拟感染过程并记录被切断不会被感染到的子树根节点即可。
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<random>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int N=300;
struct edge{
int v,r;
}a[2*(N-1)+1];
int n,h[N+1],size[N+1];
void create(int u,int v){
static int top=0;
a[++top]={v,h[u]};
h[u]=top;
}//DFS预处理
int dfs(int x){
static bool vis[N+1];
if(vis[x])return 0;
vis[x]=true;
for(int i=h[x];i>0;i=a[i].r){
size[x]+=dfs(a[i].v);
}return ++size[x];
}
int solve(){
queue<int>q,q2;
static int vis[N+1];
memset(vis,0,sizeof(vis));
q.push(1);
vis[1]=1;
while(true){
int Max=-2147483647,u=-1;
while(q.size()){
int x=q.front();q.pop();//x:已感染节点
for(int i=h[x];i>0;i=a[i].r){
if(vis[a[i].v])continue;
vis[a[i].v]=1;//先感染
q2.push(a[i].v);
if(rand()%2&&size[a[i].v]>Max){
Max=size[a[i].v];
u=a[i].v;
}
}
}if(u==-1)break;//不能切断了,跳出
vis[u]=2;//不被感染
while(q2.size()){
if(q2.front()!=u)q.push(q2.front());
q2.pop();
}
}int ans=0;
for(int i=1;i<=n;i++){//统计不被感染的人的数量
if(vis[i]==2)ans+=size[i];
}return n-ans;//n-ans:被感染的人的数量
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
srand(time(0));//事实上,实测不加也能过
scanf("%d %*d",&n);
for(int i=1;i<n;i++){
int u,v;
scanf("%d %d",&u,&v);
create(u,v);create(v,u);//邻接表存树
}dfs(1);
int ans=2147483647;
while(clock()<CLOCKS_PER_SEC*0.9){
ans=min(ans,solve());
}printf("%d\n",ans);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
后记
本人测试原题数据时,发现如果随机化贪心次数超过 $10^6$ 次,即使贪心策略只有 rand%2 (猴子算法),也大概率能过。
因此,不建议将本题作为随机化贪心练习题。
况且,正常做法是需要赋权后取模,在本题中就是依照子树大小赋权值随机化后使得子树越大随机化否定的概率越小。