什么是二维数点
顾名思义,在一个二维平面内求一个矩形内有多少个点(“点”并非指普通几何点,否则有无数个),如图。
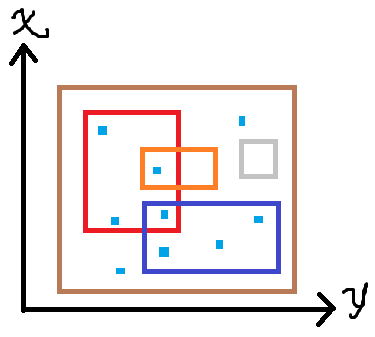
我们可以一眼看出:
- $\color{red}\colorbox{red}{1}$ 矩形内有 $1$ 个点;
- $\color{#FF8000}\colorbox{#FF8000}{1}$ 矩形内有 $1$ 个点;
- $\color{#3F48CC}\colorbox{#3F48CC}{1}$ 矩形内有 $1$ 个点;
-
$\color{#C3C3C3}\colorbox{#C3C3C3}{1}$ 矩形内没有点;
- $\color{#B97A57}\colorbox{#B97A57}{1}$ 矩形内有 $9$ 个点。
然而计算机不能如此一眼看出,那么找到矩形内点的数量的过程就是二维数点。
扫描线算法
思想如图(来源于OI Wiki):
当然,此图展现的是扫描矩形面积并,而不是二维数点,但“点”其实也可以视为 $1\times 1$ 的矩形。
扫描线的底层逻辑就是模拟一条线扫描过去,最后给出答案。
二维数点(例题:洛谷P10814)
问题形式
很有可能不是形如“给定二维平面,求某一矩形内符合要求的点的数量”,也有可能是“给一个长为 $n$ 的序列,有 $m$ 次查询,每次查区间 $[l,r]$ 中值在 $[x,y]$ 内的元素个数。”
维度压缩
其实就是将原来的静态二维问题压缩为动态一维后使用数据结构维护。
两种方案
警告
扫描线扫过的是值域。
值域(离散化)
操作
首先,当值域过大时,是肯定需要离散化的,而且是离线的离散化,即离散化所有询问。
先将所有的询问离散化,用树状数组维护权值,对于每次询问的 $l$ 和 $r$,我们在枚举到 $l-1$ 时统计当前位于区间 $[x,y]$ 内的数的数量 $a$,继续后枚举,枚举到 $r$ 时统计当前位于区间 $[x,y]$ 内的数的数量 $b$,$b-a$ 即为该次询问的答案。——Oi Wiki
但是对于例题的数据范围($10^6$),可以不离散化。
具体过程如下。
创建一个结构体记录问题:
1
2
3
struct problem{
int x,id,value;
};
$x$ 含义如题,$id$ 表示这是第几个问题,$value=\pm1$(解释见下文)。
每次读入 $l,r,x$ 后,进行如下操作:
1
2
q[l-1].push_back({x,i,-1});
q[r].push_back({x,i,1});
统计答案:
1
2
3
4
5
6
for(int i=1;i<=n;i++){
add(a[i],1);
for(int j=0;j<q[i].size();j++){
ans[q[i][j].id]+=q[i][j].value*query(q[i][j].x);
}
}
解释
如图。(为便于观察,错开了蓝色、绿色矩形,不然边框应该有重合部分)

$\color{#FF7F27} \colorbox{#FF7F27}{1}$ 橙色部分,也就是需要求的部分的答案显然等于 $\color{#22B14C}\colorbox{#22B14C}{1}$ 绿色部分减去 $\color{#00A2E8}\colorbox{#00A2E8}{1}$ 蓝色部分的答案。
那么我们令绿色、蓝色矩形的左边界为 $0$。(依题目而定,就是一个所有询问都询问不到、没有点的值)
那么抽象化一些,也就是使用 $[0,r]$ 的 合法点数减去 $[0,l-1]$ 的合法点数。
为了便于处理,我们便记录一个 $value=\pm1$ 来记录是应该进行加法还是减法。
更加具体的,也就是扫描线扫到 $l-1$ 时,先减去此时合法点数,扫描到 $r$ 时,便会抵消先前多减去的,剩下的便是答案。
时间复杂度:$\mathcal O\big((n+m)\log_2m\big)$。
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int N=2e6,M=2e6;
struct problem{
int x,id,value;
};
vector<problem>q[M+1];
int n,m,a[N+1],t[N+1],ans[N+1];
int lowbit(int x){
return x&-x;
}
void add(int x,int k){
while(x<=N){
t[x]+=k;
x+=lowbit(x);
}
}
int query(int x){
int ans=0;
while(x){
ans+=t[x];
x-=lowbit(x);
}return ans;
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",a+i);
for(int i=1;i<=m;i++){
int l,r,x;
scanf("%d %d %d",&l,&r,&x);
q[l-1].push_back({x,i,-1});
q[r].push_back({x,i,1});
}for(int i=1;i<=n;i++){
add(a[i],1);
for(int j=0;j<q[i].size();j++){
//使用.id找到对应问题,记录答案
ans[q[i][j].id]+=q[i][j].value*query(q[i][j].x);
}
}for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
/*fclose(stdin);
fclose(stdout);*/
return 0;
}
排序+记录值
你可能会看到这种写法(摘自此处):
1
2
3
4
5
6
7
8
9
10
//...
q[++cnt] = {l-1, i, x, -1};
q[++cnt] = {r, i, x, 1};
//...
sort(q + 1, q + 1 + cnt);
for (int i = 1, j = 1; i <= cnt; ++i) {
for (; j <= q[i].k; ++j) bit.add(a[j]);
ans[q[i].id] += q[i].val * bit.query(q[i].x);
}
//...
和上一种方案无思想上的差别,区别在于空间复杂度不同。但是如果加入离散化,则没有什么太大差异。
